Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Do \(\widehat{AIB}=90^0\Rightarrow\widehat{ACB}=45^0\) hoặc \(\widehat{ACB}=135^0\Rightarrow\widehat{ACD}=45^0\Rightarrow\Delta ACD\) vuông cân tại D nên DA=DC
Hơn nữa IA=IC => \(DI\perp AC\Rightarrow\) đường thẳng AC thỏa mãn điều kiện AC qua điểm M và AC vuông góc ID.
Viết phương trình đường thẳng AC : \(x-2y+9=0\)
Gọi \(A\left(2a-9;a\right)\in AC\). Do \(DA=\sqrt{2}d\left(D,AC\right)=2\sqrt{10}\) nên
\(\sqrt{\left(2a-8\right)^2+\left(a+1\right)^2}=2\sqrt{10}\Leftrightarrow a^2-6a+5=0\)
\(\Leftrightarrow\begin{cases}a=1\Rightarrow A\left(-7;1\right)\\a=5\Rightarrow A\left(1;5\right)\end{cases}\)
Theo giả thiết đầu bài \(\Rightarrow A\left(1;5\right)\)
Viết phương trình đường thẳng DB : \(x+3y+4=0\). Gọi \(B\left(-3b-4;b\right)\)
Tam giác IAB vuông tại I nên : \(\overrightarrow{IA.}\overrightarrow{IB}=0\Leftrightarrow3\left(-3b-2\right)+4\left(b-1\right)=0\Leftrightarrow b=-2\Rightarrow B\left(2;-2\right)\)
Đáp số \(A\left(1;5\right);B\left(2;-2\right)\)

Tham khảo:
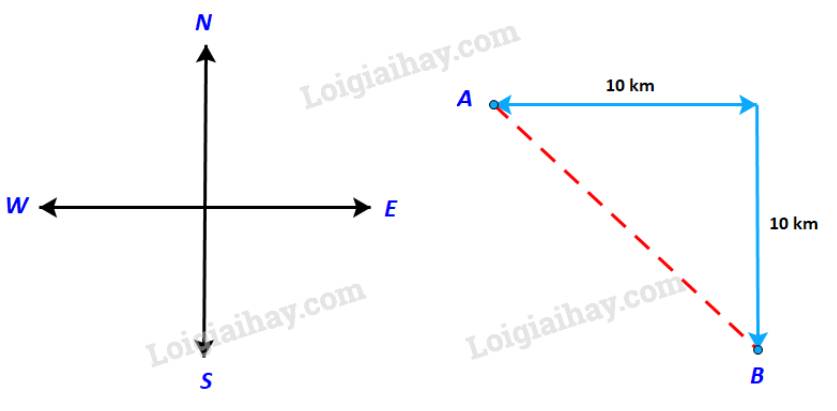
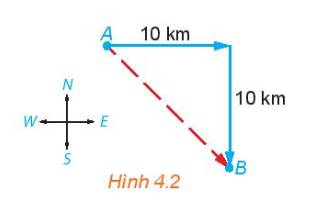
Gọi C là điểm mà tại đó tàu đổi từ hướng đông sang hướng Nam
Xét tam giác ABC ta có:
\(AC = BC = 10\;\left( {km} \right)\)
\( \Rightarrow \Delta ABC\) vuông cân tại C.
\( \Leftrightarrow \widehat A = {45^o}\)
Vậy con tàu phải đi theo hướng đông nam, góc \({45^o}\) so với hướng Đông.
Quãng đường con tàu phải đi là: \(AB = AC.\sqrt 2 = 10.\sqrt 2 \; \approx 14,142\;\left( {km} \right)\)

a) Tiêu điểm có tọa độ \((4;0)\) nên ta có \(p = 8\)
Suy ra phương trình chính tắc của parabol là: \({y^2} = 16x\)
b) Đường chuẩn có phương trình \(x = - \frac{1}{6}\), nên ta có \(p = - \frac{1}{3}\)
Suy ra phương trình chính tắc của parabol có dạng \({y^2} = - \frac{2}{3}x\)
c) Gọi phương trình chính tắc của parabol có dạng \({y^2} = 2px\)
Thay tọa độ điểm \((1;4)\) vào phương trình \({y^2} = 2px\) ta có:
\({4^2} = 2p.1 \Rightarrow p = 8\)
Vậy phương trình chính tắc của parabol là \({y^2} = 16x\)
d) Gọi \(F\left( {\frac{p}{2};0} \right)\), \(\Delta :x + \frac{p}{2} = 0\) lần lượt là tiêu điểm và phương trình đường chuẩn của parabol ta có:
\(d\left( {F,\Delta } \right) = \frac{{\left| {\frac{p}{2} + \frac{p}{2}} \right|}}{1} = 8 \Rightarrow p = 8\)
Vậy phương trình chính tắc của parabol là \({y^2} = 16x\)

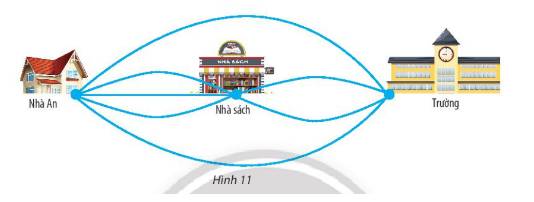
a) Việc đi từ nhà đến trường qua nhà sách được thực hiện qua hai công đoạn:
Công đoạn 1: Đi từ nhà đến nhà sách, có 3 con đường
Công đoạn 2: Đi từ nhà sách đến trường, có 2 con đường
Số cách đi từ nhà đến trường qua nhà sách có số cách là:
\(3.2 = 6\)(cách)
b) Việc đi từ nhà đến trường có 2 phương án
Phương án 1: Đi từ nhà đến trường qua nhà sách, có 6 cách thực hiện (kết quả của câu a))
Phương án 2: Đi từ nhà đến trường không qua nhà sách có 2 cách
Áp dụng quy tắc cộng, ta có số cách đi từ nhà đến trường là:
\(6 + 2 = 8\) (cách)

Theo đề bài ta có :
Lúc đi:
147x+105y+126z=17640(1)
Khi về do hướng đi ngược lại nên đoạn lên dốc và xuống dóc sẽ đổi cho nhau : x,y lần lượt là đoạn xuống dốc và đoạn lên dốc . Ta có :
105x+147y+126z=26460(2)
Lấy (1)+(2) Ta rút gọn nên được : x+y+z=175 km(đó chính là quảng đường AB :))