
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

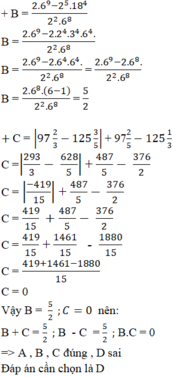

a, \(139\frac{5}{7}:\frac{2}{3}−138\frac{2}{7}:\sqrt{\frac{4}{9}} \)
= \(139\frac{5}{7}:\frac{2}{3}−138\frac{2}{7}:\frac{2}{3}\)
= \((139\frac{5}{7}−138\frac{2}{7}):\frac{2}{3}\)
= \(1\frac{3}{7}:\frac{2}{3}\)
= \(2\frac{1}{7}\)
b, \((\frac{-5}{11}:\frac{13}{18}-\frac{5}{11}:\frac{13}{5})+\frac{-1}{33} \)
= \((\frac{5}{11}.\frac{-18}{13}-\frac{5}{11}.\frac{5}{13})+\frac{-1}{33}\)
= \([\frac{5}{11}.(\frac{-18}{13}-\frac{5}{13})]+\frac{-1}{33}\)
= \((\frac{5}{11}.\frac{-23}{13})+\frac{-1}{33}\)
= \(\frac{-155}{143}+\frac{-1}{33}\)
= \(\frac{-358}{429} \)
c, \(∣97\frac{2}{3}-125\frac{3}{5}∣+97\frac{2}{3}-125\frac{3}{5} \)
= \(∣\frac{-419}{15}∣+97\frac{2}{3}-125\frac{3}{5}\)
= \(\frac{419}{15}+97\frac{2}{3}-125\frac{3}{5}\)
= \(0\)
Tick cho mình nha!!!
Chúc bạn học tốt.

a) S = 1.2 + 2.3 + 3.4 + ... + 99.100
S có thể được viết lại thành:
S = 1(2 - 0) + 2(3 - 1) + 3(4 - 2) + ... + 99(100 - 98)
= 1.2 - 0 + 2.3 - 1 + 3.4 - 2 + ... + 99.100 - 98
= (1.2 + 2.3 + 3.4 + ... + 99.100) - (0 + 1 + 2 + ... + 98)
Để tính tổng 1.2 + 2.3 + 3.4 + ... + 99.100, ta sử dụng công thức:
S = n(n+1)(2n+1)/6
Với n = 99, ta có:
S = 99.100.199/6 = 331650
Tính tổng 0 + 1 + 2 + ... + 98, ta sử dụng công thức:
S = n(n+1)/2
Với n = 98, ta có:
S = 98.99/2 = 4851
Do đó, S = 331650 - 4851 = 326799
b) B = 4924.12517.28−530.749.45529.162.748
B có thể được viết lại thành:
B = (4924.12517.28) / (530.749.45529.162.748)
B = (4924 / 530) . (12517 / 749) . (28 / 45529) . (162 / 162) . (748 / 748)
B = 9.17.28/45529 = 2^2 . 3^2 . 17 / 45529
B = 108 / 45529
c) C = (13+132+133+134).35+(135+136+137+138).39+...+(1397+1398+1399+13100).3101
C = (13(1 + 13 + 13^2 + 13^3)) . 3^5 + (13^5(1 + 13 + 13^2 + 13^3)) . 3^9 + ... + (13^97(1 + 13 + 13^2 + 13^3)) . 3^101
C = (1 + 13 + 13^2 + 13^3) . (13^5 . 3^5 + 13^9 . 3^9 + ... + 13^97 . 3^101)
C = 80 . (13^5 . 3^5 + 13^9 . 3^9 + ... + 13^97 . 3^101)
C = 80 . (13^5 . 3^4 . 3 + 13^9 . 3^8 . 3 + ... + 13^97 . 3^96 . 3)
C = 80 . (13^6 . 3^5 + 13^10 . 3^9 + ... + 13^98 . 3^97)
C = 80 . 3^5 (13^6 + 13^10 + ... + 13^98)
d) D = 3 - 3^2 + 3^3 - 3^4 + ... + 3^2017 - 3^2018
D = (3 - 3^2) + (3^3 - 3^4) + ... + (3^

Bài 2:
1: \(5^n+5^{n+2}=650\)
\(\Leftrightarrow5^n\cdot26=650\)
\(\Leftrightarrow5^n=25\)
hay x=2
2: \(32^{-n}\cdot16^n=1024\)
\(\Leftrightarrow\dfrac{1}{32^n}\cdot16^n=1024\)
\(\Leftrightarrow\left(\dfrac{1}{2}\right)^n=1024\)
hay n=-10
13: \(9\cdot27^n=3^5\)
\(\Leftrightarrow3^{3n}=3^5:3^2=3^3\)
=>3n=3
hay n=1

a, \(125^3:5^7=\left(5^3\right)^3:5^7=5^9:5^7=5^2\)
b, \(\left(\dfrac{2}{7}\right)^{18}:\left(\dfrac{4}{49}\right)^5:\left(\dfrac{8}{343}\right)^2\)
= \(\left(\dfrac{2}{7}\right)^{18}:\left(\dfrac{2^2}{7^2}\right)^5:\left(\dfrac{2^3}{7^3}\right)^2\)
= \(\left(\dfrac{2}{7}\right)^{18}:\left[\left(\dfrac{2}{7}\right)^2\right]^5:\left[\left(\dfrac{2}{7}\right)^3\right]^2\)
=\(\left(\dfrac{2}{7}\right)^{18}:\left(\dfrac{2}{7}\right)^{10}:\left(\dfrac{2}{7}\right)^6\)
= \(\left(\dfrac{2}{7}\right)^{18-10-6}=\left(\dfrac{2}{7}\right)^2\)
c, \(3-\left(\dfrac{-7}{9}\right)^0+\left(\dfrac{1}{3}\right)^5.3^5\)
= 3 - 1 +\(\left[\left(\dfrac{1}{3}\right)^5.3^5\right]\)
= 2 + 1=3
d, \(\dfrac{45^{10}.5^{20}}{75^{15}}=\dfrac{\left(9.5\right)^{10}.5^{20}}{\left(25.3\right)^{15}}=\dfrac{\left(3^2\right)^{10}.5^{10}.5^{20}}{\left(5^2\right)^{15}.3^{15}}\)
= \(\dfrac{3^{20}.5^{30}}{5^{30}.3^{15}}=3^5\)