Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A(m-1;-1); B(2;2-2m); C(m+3;3)
\(\overrightarrow{AB}=\left(2-m+1;2-2m+1\right)\)
=>\(\overrightarrow{AB}=\left(3-m;3-2m\right)\)
\(\overrightarrow{AC}=\left(m+3-m+1;3+1\right)\)
=>\(\overrightarrow{AC}=\left(4;4\right)\)
Để A,B,C thẳng hàng thì \(\dfrac{3-m}{4}=\dfrac{3-2m}{4}\)
=>3-m=3-2m
=>m=0
\(\left\{{}\begin{matrix}\overrightarrow{AB}=\left(3-m;3-2m\right)\\\overrightarrow{AC}=\left(4;4\right)\end{matrix}\right.\)
3 điểm A;B;C thẳng hàng khi và chỉ khi \(\overrightarrow{AB}=k\overrightarrow{AC}\) với \(k\ne0\)
Hay \(\dfrac{3-m}{4}=\dfrac{3-2m}{4}\Rightarrow m=0\)

bn thiếu các dấu vec tơ nha
ta có : \(\overrightarrow{AB}\left(3-m;3-2m\right)\) và \(\overrightarrow{AC}\left(-2;2\right)\)
để : \(A;B;C\) thẳng hàng khi và chỉ khi \(\overrightarrow{AB}\) cùng phương với \(\overrightarrow{AC}\)
tương đương \(\dfrac{3-m}{-2}=\dfrac{3-2m}{2}\) \(\Leftrightarrow\dfrac{m-3}{2}=\dfrac{3-2m}{2}\)
\(\Leftrightarrow m-3=3-2m\Leftrightarrow3m=6\Leftrightarrow m=\dfrac{6}{3}=2\)
vậy \(m=2\) thì 3 điểm \(A;B;C\) thẳng hàng

a/ \(\overrightarrow{AB}=\left(4;8\right)\Rightarrow\) đường thẳng AB có 1 vtpt là \(\left(2;-1\right)\)
Phương trình AB:
\(2\left(x-3\right)-\left(y-4\right)=0\Leftrightarrow2x-y-2=0\)
A;P;B thẳng hàng \(\Rightarrow P\in AB\Rightarrow P\left(x;2x-2\right)\)
\(\overrightarrow{AP}=\left(x+1;2x+2\right)\Rightarrow AP^2=\left(x+1\right)^2+\left(2x+2\right)^2=5\left(x+1\right)^2\)
\(\Rightarrow5\left(x+1\right)^2=\left(3\sqrt{5}\right)^2\Rightarrow\left(x+1\right)^2=9\Rightarrow\left[{}\begin{matrix}x=2\\x=-4\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}P\left(2;2\right)\\P\left(-4;-10\right)\end{matrix}\right.\)
Gọi \(M\left(x;0\right)\)
b/ \(\overrightarrow{AM}=\left(x+1;4\right)\Rightarrow MA=\sqrt{\left(x+1\right)^2+4^2}\)
\(\overrightarrow{MB}=\left(3-x;4\right)\Rightarrow MB=\sqrt{\left(3-x\right)^2+4^2}\)
\(T=MA+MB=\sqrt{\left(x+1\right)^2+4^2}+\sqrt{\left(3-x\right)^2+4^2}\)
Áp dụng BĐT Mincopxki:
\(T\ge\sqrt{\left(x+1+3-x\right)^2+\left(4+4\right)^2}=4\sqrt{5}\)
\(T_{min}=4\sqrt{5}\) khi \(x+1=3-x\Rightarrow x=1\Rightarrow M\left(1;0\right)\)
c/ Tương tự như câu b:
\(MB+MC=\sqrt{\left(3-x\right)^2+4^2}+\sqrt{\left(x-2\right)^2+5^2}\)
\(MB+MC\ge\sqrt{\left(3-x+x-2\right)^2+\left(4+5\right)^2}=\sqrt{82}\)
Dấu "=" xảy ra khi \(\frac{3-x}{4}=\frac{x-2}{5}\Rightarrow x=\frac{23}{9}\Rightarrow M\left(\frac{23}{9};0\right)\)

Lời giải:
\(\overrightarrow{AB}=(-4,2)\)
\(\overrightarrow{u_d}=(2,-1)\)
Để 2 đường thẳng cắt nhau thì \(\frac{-4}{2}\neq \frac{2}{-1}\) (vô lý)
Do đó 2 đường thẳng không thể cắt nhau với mọi $m$. Đáp án D
PTTQ của d : \(1\left(x-m\right)+2\left(y-1\right)=0\)
\(\Leftrightarrow x+2y-m-2=0\)
Để d cắt AB thì A và B nằm khác phía so với d hoặc là một trong 2 điểm A và B nằm trên d . Nên ta có :
\(\left(1+4-m-2\right)\left(-3+8-m-2\right)\le0\)
\(\Leftrightarrow\left(-m+3\right)\left(-m+3\right)\le0\)
\(\Leftrightarrow m=3\)
Chọn B

a) \(\overrightarrow{AB}\left(2;-2\right)\); \(\overrightarrow{CA}=\left(4;-4\right)\).
Vì \(\dfrac{2}{4}=\dfrac{-2}{-4}\) nên \(\overrightarrow{AB};\overrightarrow{CA}\) cùng phương . Suy ra ba điểm A, B, C thẳng hàng.
\(\overrightarrow{AB}\left(2;1\right)\); \(\overrightarrow{AC}\left(m+3;2m\right)\).
3 điểm A, B, C thẳng hàng nên hai véc tơ \(\overrightarrow{AB},\overrightarrow{AC}\) cùng phương.
Suy ra: \(\dfrac{m+3}{2}=\dfrac{2m}{1}\Leftrightarrow m+3=4m\)\(\Leftrightarrow m=1\).
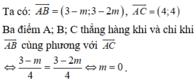
Chọn C
Vecto AB = (3 - m; 3 - 2m)
Vecto AC = (-2; 2)
A, B, C thẳng hàng
<=> vecto AB và vecto AC cùng phương
<=> (3 - m)/(-2) = (3 - 2m)/2
<=> m - 3 = 3 - 2m
<=> 3m = 6
=> m = 2
-> A