NL
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NH
0
24 tháng 9 2015
Theo mình:
Tam giác ABC vuông tại A
---> BA là đường cao ( BA vuông góc AC)
---> S tam giác ABC = \(\frac{a.h}{2}=\frac{AC.BC}{2}=\frac{4.3}{2}=6cm^2\)
Pytago tam giác ABC vuông tại A:
BC2 = BA2 + AC2
= 9 + 16
= 25
BC= 5 cm
Vì AH cũng là đường cao của tam giác ABC
----> AH = \(\frac{2.S}{a}=\frac{2.6}{BC}=\frac{12}{5}=2,4cm\)
Theo mình thì mình làm vậy á, nếu mình làm sai thì bạn sửa giùm mình nha
NT
3 tháng 8 2016
xét tam giác ABC vuông ở A co \(BC^2=AB^2+AC^2\left(pitago\right)\)
\(BC^2=9+16=25\Rightarrow BC=5\)
xet tgABH va tgCBA co goc B chung ; gAHB=gBAC =90
=>tgABH đồng dạng tgCBA =>\(\frac{AH}{AC}=\frac{AB}{BC}\Leftrightarrow\frac{AH}{4}=\frac{3}{5}\Rightarrow AH=\frac{3\cdot4}{5}=\frac{12}{5}\)
ND
0
AQ
2
14 tháng 3 2023
3:
a: AE/AD=9/6=3/2
AD/AC=6/12=1/2
b: Xét ΔADE và ΔABC có
AD/AB=AE/AC
góc A chung
=>ΔADE đồng dạng vơi ΔABC
c: IB/IC=AB/AC=AD/AE
=>IB*AE=IC*AD
9 tháng 5 2023
a: Xét ΔHBA vuông tại H và ΔABC vuông tại A có
góc B chung
=>ΔHBA đồng dạng với ΔABC
b: \(BC=\sqrt{3^2+4^2}=5\left(cm\right)\)
AH=3*4/5=2,4cm
MP
9 tháng 5 2023
a. Xét ΔHBA và ΔABC có:
\(\widehat{H}=\widehat{A}\) = 900 (gt)
\(\widehat{B}\) chung
\(\Rightarrow\) ΔHBA \(\sim\) ΔABC (g.g)
b. Vì ΔABC vuông tại A
Theo đ/lí Py - ta - go ta có:
BC2 = AB2 + AC2
BC2 = 32 + 42
\(\Rightarrow\) BC2 = 25 cm
\(\Rightarrow\) BC = \(\sqrt{25}=5\) cm
Ta lại có: ΔHBA \(\sim\) ΔABC
\(\dfrac{AH}{CA}=\dfrac{BA}{BC}\)
\(\Leftrightarrow\dfrac{AH}{4}=\dfrac{3}{5}\)
\(\Rightarrow\) AH = 2,4 cm
CM
7 tháng 9 2019
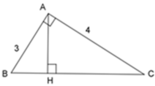
Áp dụng định lý Pytago vào tam giác vuông ABC ta có:
A B 2 + A C 2 = B C 2 ⇔ 3 2 + 4 2 = B C 2
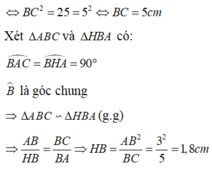
Ta có tam giác vuông ABC=> AB2+AC2=BC2(do BC là cạnh huyền)
Mà AB=3cm; AC=4cm ta đc
32+42=BC2
=>9+16=BC2
=>BC=5(cm)
Diện tích hình tam giác là: 3.4/2=6(cm2)
Độ dài AH là: 6.2/5=2,4cm
Vậy AH=2,4cm
cuối cùng là = bao nhiu?