K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NT
2
KN
18 tháng 2 2020
Ta có: \(a\left(b^2-1\right)\left(c^2-1\right)+b\left(a^2-1\right)\left(c^2-1\right)+c\left(a^2-1\right)\left(b^2-1\right)\)
\(=a\left(b^2c^2-b^2-c^2+1\right)+b\left(a^2c^2-a^2-c^2+1\right)\)
\(+c\left(a^2b^2-a^2-b^2+1\right)\)
\(=ab^2c^2-ab^2-ac^2+a+ba^2c^2-a^2b-bc^2+b\)
\(+ca^2b^2-a^2c-b^2c+c\)
\(=\left(ab^2c^2+ba^2c^2+ca^2b^2\right)+\left(a+b+c\right)\)
\(-\left(ab^2+ac^2+a^2b+bc^2+a^2c+b^2c\right)\)
\(=abc\left(bc+ac+ab\right)+\left(a+b+c\right)\)\(-\left[ab\left(a+b\right)+bc\left(b+c\right)+ca\left(c+a\right)\right]\)
\(=abc\left(bc+ac+ab\right)+\left(a+b+c\right)+3abc\)\(-\left[ab\left(a+b+c\right)+bc\left(a+b+c\right)+ca\left(a+b+c\right)\right]\)
\(=abc\left(bc+ac+ab\right)+\left(a+b+c\right)+3abc\)\(-\left(a+b+c\right)\left(ab+bc+ca\right)\)
\(=abc\left(bc+ac+ab\right)+abc+3abc\)\(-abc\left(ab+bc+ca\right)=4abc\)
Vậy \(a\left(b^2-1\right)\left(c^2-1\right)+b\left(a^2-1\right)\left(c^2-1\right)+c\left(a^2-1\right)\left(b^2-1\right)=4abc\)(đpcm)
H
2 tháng 4 2021
Ta có:
\(a^2+b^2+c^2=ab+bc+ca\\ \Leftrightarrow2a^2+2b^2+2c^2-2ab-2bc-2ca=0\\ \Leftrightarrow\left(a^2-2ab+b^2\right)+\left(b^2-2bc+c^2\right)+\left(c^2-2ca+a^2\right)=0\\ \Leftrightarrow\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2=0\)
Mà \(\left(a-b\right)^2,\left(b-c\right)^2,\left(c-a\right)^2\ge0\Rightarrow\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2\ge0\)
\(\Rightarrow\left(a-b\right)^2=\left(b-c\right)^2=\left(c-a\right)^2=0\\ \Leftrightarrow a=b=c\)
Lại có: \(a+b+c=3\Rightarrow a=b=c=1\)
\(\Rightarrow M=1^{2016}+1^{2015}+1^{2020}=1+1+1=3\)
TD
0
BN
2
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 8 2021
\(\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2\ge0\) ; \(\forall a;b;c\)
\(\Leftrightarrow a^2+b^2+c^2\ge ab+bc+ca\)
\(\Rightarrow ab+bc+ca\le1\)
\(\Rightarrow P_{max}=1\) khi \(a=b=c\)
Lại có:
\(\left(a+b+c\right)^2\ge0\) ; \(\forall a;b;c\)
\(\Leftrightarrow a^2+b^2+c^2+2\left(ab+bc+ca\right)\ge0\)
\(\Leftrightarrow ab+bc+ca\ge-\dfrac{a^2+b^2+c^2}{2}=-\dfrac{1}{2}\)
\(P_{min}=-\dfrac{1}{2}\) khi \(a+b+c=0\)
NV
Nguyễn Việt Lâm
Giáo viên
6 tháng 4 2021
Đề bài sai, phản ví dụ: \(a=b=0,c=1\)
BĐT này chỉ đúng khi a;b;c là độ dài 3 cạnh của 1 tam giác
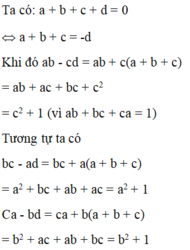
\(ab+bc+ac\le1\)
Ta có \(a^2+b^2+c^2=1\)
\(\Rightarrow ab+bc+ac\le a^2+b^2+c^2\)
Áp dụng bất đẳng thức Cô - si
\(\Rightarrow\left\{\begin{matrix}a^2+b^2\ge2\sqrt{a^2b^2}=2ab\\b^2+c^2\ge2\sqrt{b^2c^2}=2bc\\a^2+c^2\ge2\sqrt{a^2c^2}=2ac\end{matrix}\right.\)
Cộng theo từng vế
\(\Rightarrow2\left(a^2+b^2+c^2\right)\ge2\left(ab+bc+ac\right)\)
\(\Rightarrow a^2+b^2+c^2\ge ab+bc+ac\)
\(\Leftrightarrow1\ge ab+bc+ac\) ( đpcm )
phải là \(ab+bc+ca\le1\) nha bởi vì dấu "=" vẫn xảy ra đó.
+ \(\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2\ge0\forall a,b,c\)
\(\Leftrightarrow\left(a^2-2ab+b^2\right)+\left(b^2-2bc+c^2\right)+\left(c^2-2ca+a^2\right)\ge0\)
\(\Leftrightarrow2\left(a^2+b^2+c^2\right)-2\left(ab+bc+ca\right)\ge0\)
\(\Leftrightarrow2\left(ab+bc+ca\right)\le2\left(a^2+b^2+c^2\right)\)
\(\Leftrightarrow ab+bc+ca\le1\)
Dấu "=" xảy ra \(\Leftrightarrow\left\{{}\begin{matrix}a=b=c\\a^2+b^2+c^2=1\end{matrix}\right.\Leftrightarrow a=b=c=\pm\sqrt{\frac{1}{3}}\)