Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) √2 cos(x - π/4)
= √2.(cosx.cos π/4 + sinx.sin π/4)
= √2.(√2/2.cosx + √2/2.sinx)
= √2.√2/2.cosx + √2.√2/2.sinx
= cosx + sinx (đpcm)
b) √2.sin(x - π/4)
= √2.(sinx.cos π/4 - sin π/4.cosx )
= √2.(√2/2.sinx - √2/2.cosx )
= √2.√2/2.sinx - √2.√2/2.cosx
= sinx – cosx (đpcm).
cho 3 góc A, B, C của tam giác lập thành 1 CSN có công bội q=2. Tính gtbt \(M=cos^2A+cos^2B+cos^2C\)

Không mất tính tổng quát, giả sử \(A< B< C\Rightarrow\left\{{}\begin{matrix}B=A.q=2A\\C=A.q^2=4A\end{matrix}\right.\)
\(A+B+C=180^0\Rightarrow A+2A+4A=180^0\)
\(\Rightarrow7A=180^0\Rightarrow\left\{{}\begin{matrix}A=\dfrac{180^0}{7}\\B=\dfrac{360^0}{7}\\C=\dfrac{720^0}{7}\end{matrix}\right.\)
Thế vào bấm máy biểu thức M. Nhưng tại sao người ta cho xấu vậy nhỉ?

heo me tim gtnn gtln cua bieu thuc:asinx + bcosx (a,b la hang so,a^2+b^2=/o)? | Yahoo Hỏi & Đáp

Đkxđ: \(x\in R\).
\(cos2x-cos3x+cos4x=0\Leftrightarrow\left(cos2x+cos4x\right)-cos3x=0\)
\(\Leftrightarrow2cos3x.cosx-cos3x=0\)
\(\Leftrightarrow cos3x\left(2cos2x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos3x=0\\2cos2x-1=0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}cos3x=0\\cos2x=\dfrac{1}{2}\end{matrix}\right.\)
\(cos3x=0\Leftrightarrow3x=\dfrac{\pi}{2}+k\pi\Leftrightarrow x=\dfrac{\pi}{6}+\dfrac{k\pi}{3}\)
\(cos2x=\dfrac{1}{2}\Leftrightarrow\left[{}\begin{matrix}2x=\dfrac{\pi}{3}+k2\pi\\2x=-\dfrac{\pi}{3}+k2\pi\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}+k\pi\\x=-\dfrac{\pi}{6}+k\pi\end{matrix}\right.\)
\(\dfrac{sinB}{sinC}=2cosA\Leftrightarrow sinB=2cosA.sinC\)
\(\Leftrightarrow sinB=sin\left(A+C\right)+sin\left(C-A\right)\)
\(\Leftrightarrow sinB=sin\left(\pi-\left(A+C\right)\right)+sin\left(C-A\right)\)
\(\Leftrightarrow sinB=sinB+sin\left(C-A\right)\)
\(\Leftrightarrow sin\left(C-A\right)=0\) (1)
Do A, C là số đo các góc trong tam giác nên từ (1) suy ra:
\(C=A\) hay tam giác ABC cân.

Ta có: \(\sin \left( {a + b} \right)\sin \left( {a - b} \right) = \left( {\sin a\cos b + \cos a\sin b} \right).\left( {\sin a\cos b - \cos a\sin b} \right)\)
\( = {\left( {\sin a\cos b} \right)^2} - {\left( {\cos a\sin b} \right)^2} = {\sin ^2}a\left( {1 - {{\sin }^2}b} \right) - \left( {1 - {{\sin }^2}a} \right){\sin ^2}b\)
\({\sin ^2}a - {\sin ^2}b = {\cos ^2}b\left( {1 - {{\cos }^2}a} \right) - {\cos ^2}a\left( {1 - {{\cos }^2}b} \right) = {\cos ^2}b - {\cos ^2}a\;\) (đpcm)

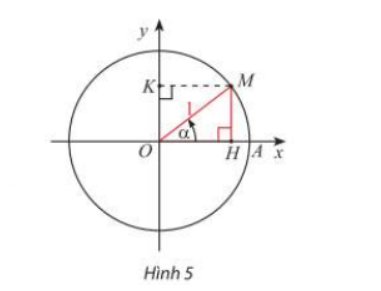
a) Do \(\begin{array}{l}\sin \alpha = MH \Rightarrow {\sin ^2}\alpha = M{H^2}\\\cos \alpha = OH \Rightarrow {\cos ^2}\alpha = O{H^2}\end{array}\)
Áp dụng định lý Py – Ta – Go vào tam giác OMH vuông tại H ta có:
\(\begin{array}{l}M{H^2} + O{H^2} = O{M^2} = 1\\ \Rightarrow {\sin ^2}\alpha + {\cos ^2}\alpha = 1\end{array}\)
b) Chia cả hai vế cho \({\cos ^2}\alpha \), ta được:
\(\begin{array}{l}\frac{{{{\sin }^2}\alpha }}{{{{\cos }^2}\alpha }} + \frac{{{{\cos }^2}\alpha }}{{{{\cos }^2}\alpha }} = \frac{1}{{{{\cos }^2}\alpha }}\\ \Leftrightarrow {\tan ^2}\alpha + 1 = \frac{1}{{{{\cos }^2}\alpha }}\end{array}\)
c) Chia cả hai vế cho \({\sin ^2}\alpha \), ta được:
\(\begin{array}{l}\frac{{{{\sin }^2}\alpha }}{{{{\sin }^2}\alpha }} + \frac{{{{\cos }^2}\alpha }}{{{{\sin }^2}\alpha }} = \frac{1}{{{{\sin }^2}\alpha }}\\ \Leftrightarrow {\cot ^2}\alpha + 1 = \frac{1}{{{{\sin }^2}\alpha }}\end{array}\)

Xét các vec tơ đơn vị \(\frac{\overrightarrow{AB}}{AB};\frac{\overrightarrow{BC}}{BC};\frac{\overrightarrow{CA}}{CA}\) trên các cạnh AB, BC, CA của tam giác ABC
Có \(0\le\left(\frac{\overrightarrow{AB}}{AB};\frac{\overrightarrow{BC}}{BC};\frac{\overrightarrow{CA}}{CA}\right)^2=3-2\left(\cos A+\cos B+\cos C\right)\)
Suy ra \(\cos A+\cos B+\cos C\le\frac{3}{2}\) => Điều cần chứng minh
a) \(cos\left(A+B\right)+cosC=0\)
\(\Leftrightarrow cos\left(\pi-C\right)+cosC=0\)
\(\Leftrightarrow-cosC+cosC=0\)
\(\Leftrightarrow0=0\left(đúng\right)\)
\(\Leftrightarrow dpcm\)
b) \(cos\left(\dfrac{A+B}{2}\right)=sin\dfrac{C}{2}\)
\(\Leftrightarrow cos\left(\dfrac{\pi-C}{2}\right)=sin\dfrac{C}{2}\)
\(\Leftrightarrow cos\left(\dfrac{\pi}{2}-\dfrac{C}{2}\right)=sin\dfrac{C}{2}\)
\(\Leftrightarrow sin\dfrac{C}{2}=sin\dfrac{C}{2}\left(đúng\right)\)
\(\Leftrightarrow dpcm\)
c) \(cos\left(A-B\right)+cos\left(2B+C\right)=0\left(1\right)\)
Ta có : \(A+B+C=\pi\)
\(\Leftrightarrow2B+C=\pi-A+B\)
\(\Leftrightarrow2B+C=\pi-\left(A-B\right)\)
\(\left(1\right)\Leftrightarrow cos\left(A-B\right)+cos\left[\pi-\left(A-B\right)\right]=0\)
\(\Leftrightarrow cos\left(A-B\right)-cos\left(A-B\right)=0\)
\(\Leftrightarrow0=0\left(đúng\right)\)
\(\Leftrightarrow dpcm\)