Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Sai đề:
Thử với \(A=B=C=60^0\) thay vào ta được:
\(-\dfrac{3}{2}=-1+\dfrac{1}{8}\) (vô lí)

3/
\(cos4A+cos4B+cos4C=2cos\left(2A+2B\right).cos\left(2A-2B\right)+2cos^22C-1\)
\(=2cos2C.cos\left(2A-2B\right)+2cos^22C-1\)
\(=2cos2C\left(cos\left(2A-2B\right)+cos2C\right)-1\)
\(=2cos2C\left(cos\left(2A-2B\right)+cos\left(2A+2B\right)\right)-1\)
\(=4cos2A.cos2B.cos2C-1\Rightarrow\left\{{}\begin{matrix}a=-1\\b=4\end{matrix}\right.\)
4/
\(cos^2A+cos^2B+cos^2C=\frac{1}{2}+\frac{1}{2}cos2A+\frac{1}{2}+\frac{1}{2}cos2B+\frac{1}{2}+\frac{1}{2}cos2C\)
\(=\frac{3}{2}+\frac{1}{2}\left(cos2A+cos2B+cos2C\right)\)
\(=\frac{3}{2}+\frac{1}{2}\left[2cos\left(A+B\right).cos\left(A-B\right)+2cos^2C-1\right]\)
\(=1+\frac{1}{2}\left(-2cosC.cos\left(A-B\right)+2cos^2C\right)\)
\(=1-cosC\left(cos\left(A-B\right)-cosC\right)\)
\(=1-cosC\left(cos\left(A-B\right)+cos\left(A+B\right)\right)\)
\(=1-2cosA.cosB.cosC\) \(\Rightarrow\left\{{}\begin{matrix}a=1\\b=-2\end{matrix}\right.\)
1/ \(sinA+sinB+sin2\frac{C}{2}=2sin\frac{A+B}{2}cos\frac{A-B}{2}+2sin\frac{C}{2}cos\frac{C}{2}\)
\(=2cos\frac{C}{2}.cos\frac{A-B}{2}+2cos\frac{A+B}{2}.cos\frac{C}{2}=2cos\frac{C}{2}\left(cos\frac{A-B}{2}+cos\frac{A+B}{2}\right)\)
\(=4cos\frac{A}{2}cos\frac{B}{2}cos\frac{C}{2}\Rightarrow\left\{{}\begin{matrix}a=0\\b=4\end{matrix}\right.\)
2/ \(sin4A+sin4B+sin4C=2sin\left(2A+2B\right)cos\left(2A-2B\right)+2sin2C.cos2C\)
\(=-2sin2C.cos\left(2A-2B\right)+2sin2C.cos2C\)
\(\)\(=2sin2C\left(cos2C-cos\left(2A-2B\right)\right)\)
\(=-4sin2C.sin\left(C+A-B\right)sin\left(C-A+B\right)\)
\(=-4sin2A.sin2B.sin2C\Rightarrow\left\{{}\begin{matrix}a=0\\b=-4\end{matrix}\right.\)

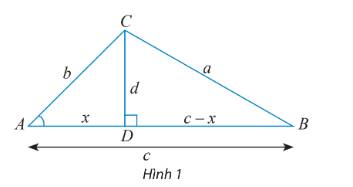
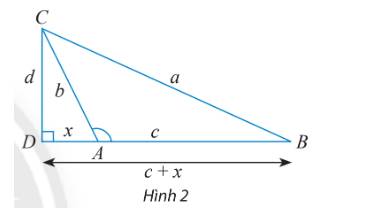
a) ? = x vì \(\cos A = \frac{{AD}}{{AC}} = \frac{x}{b} \Rightarrow ? = x.\)
b) Xét tam giác vuông BCD, ta có: \({a^2} = {d^2} + {(c + x)^2} = {d^2} + {x^2} + {c^2} + 2xc\) (1)
Xét tam giác vuông ACD, ta có: \({b^2} = {d^2} + {x^2} \Rightarrow {d^2} = {b^2} - {x^2}\) (2)
\(\cos A = - \cos \widehat {DAC} = - \frac{x}{b} \Rightarrow x = - b\cos A.\) (3)
Thay (2) và (3) vào (1), ta có: \({a^2} = {b^2} + {c^2} - 2bc\cos A\)
c) Ta có: \({a^2} = {b^2} + {c^2} - 2bc\cos A\)
Mà \(\widehat A = {90^o} \Rightarrow \cos A = \cos {90^o} = 0.\)
\( \Rightarrow {a^2} = {b^2} + {c^2}\)

\(\dfrac{cosa+cos5a+cos3a}{sina+sin5a+sin3a}=\dfrac{2cos3a.cos2a+cos3a}{2sin3a.cos2a+sin3a}\)
\(=\dfrac{cos3a\left(2cos2a+1\right)}{sin3a\left(2cos2a+1\right)}=\dfrac{cos3a}{sin3a}=cot3a\)
\(\left(\dfrac{cosa}{sinb}+\dfrac{sina}{cosb}\right)\left(\dfrac{1-cos4b}{cos\left(a-b\right)}\right)=\dfrac{\left(cosa.cosb+sina.sinb\right)}{sinb.cosb}.\dfrac{2sin^22b}{cos\left(a-b\right)}\)
\(=\dfrac{cos\left(a-b\right)}{\dfrac{1}{2}sin2b}.\dfrac{2sin^22b}{cos\left(a-b\right)}=4sin2b\)
\(\cos 4A+\cos 4B+\cos 4C=(\cos 4A+\cos 4B)+\cos 4C\)
\(=2\cos (2A+2B)\cos (2A-2B)+2\cos ^22C-1\)
\(=2\cos (2\pi -2C)\cos (2A-2B)+2\cos ^22C-1\)
\(=2\cos 2C\cos (2A-2B)+2\cos ^2C-1\)
\(=2\cos 2C[\cos (2A-2B)+\cos 2C]-1\)
\(=2\cos 2C[\cos (2A-2B)+\cos (2A+2B)]-1\)
\(=2\cos 2C.2\cos 2A\cos (-2B)-1\)
\(=-4\cos 2A\cos 2B\cos 2C-1\)