Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

ôi dào , bài nhu thế này ta ko bt làm , phải làm sao đây ....?

Vì ba đường trung trực của tam giác đồng quy nên D thuộc đường trung trực của cạnh BC. Mặt khác đường trung trực của cạnh BC đi qua trung điểm của BC nên D là trung điểm của cạnh BC.

Lời giải:
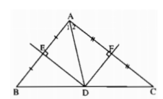
a. Xét tam giác $ABE$ và $DBE$ có:
$AB=DB$ (gt)
$BE$ chung
$\widehat{BAE}=\widehat{BDE}=90^0$
$\Rightarrow \triangle ABE=\triangle DBE$ (ch-cgv)
b.
Vì tam giác bằng nhau phần a suy ra $\widehat{ABE}=\widehat{DBE}$
Do đó $BE$ là phân giác $\widehat{ABD}$
Mà $ABD$ là tam giác cân tại $B$ nên phân giác $BE$ đồng thời là trung trực
$\Rightarrow BE$ là trung trực của $AD$
-----
Hoặc bạn có thể chỉ ra:
$BA=BD$
$EA=ED$
$\Rightarrow BE$ là trung trực $AD$
c.
Xét tam giác $AEF$ và $DEC$ có:
$\widehat{AEF}=\widehat{DEC}$ (đối đỉnh)
$AE=ED$ (cmt)
$\widehat{FAE}=\widehat{CDE}=90^0$
$\Rightarrow \triangle AEF=\triangle DEC$ (g.c.g)
$\Rightarrow AF=DC$
Ta có:
$BA=BD$
$AF=DC$
$\Rightarrow BA+AF=BD+DC$ hay $BF=BC$ nên $BCF$ cân tại $B$

Vì D nằm giữa A và C →AC=AD+DC→AC=AD+DC
Mà D∈D∈ trung trực của BC
→DB=DC→DB=DC
Ta có : ΔABDΔABD có AB<AD+BD=AD+DC=ACAB<AD+BD=AD+DC=AC
Vì D nằm giữa A và C →AC=AD+DC→AC=AD+DC
Mà D∈D∈ trung trực của BC
→DB=DC→DB=DC
Ta có : ΔABD có AB<AD+BD=AD+DC=AC