Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1.
a) Xét ΔABC có \(\frac{AD}{AB}=\frac{AE}{AC}\left(gt\right)\) => DE//BC
=> \(\frac{AD}{BD}=\frac{AE}{EC}\) (đ/lí Ta-lét)
b) Ta có: AB = AD + BD = 2 + 1 = 3 (cm)
Xét ΔABC có DE//BC => \(\frac{AD}{AB}=\frac{DE}{BC}=\frac{2}{3}\) (hệ quả đ/lí Ta-lét)
=> BC = \(\frac{AB.DE}{AD}=\frac{3.3}{2}=4,5\left(cm\right)\)
2.
a) Ta có: BD = AB - AD = 11 - 4 = 7 (cm)
Xét ΔABC có DE//BC (gt), theo đ/lí Ta-lét có: \(\frac{AE}{EC}=\frac{AB}{BD}=\frac{4}{7}\)
b) Ta có: \(\frac{AE}{EC}=\frac{4}{7}\left(cmt\right)\) => \(\frac{AE}{EC-AE}=\frac{4}{7-4}\Rightarrow\frac{AE}{1,5}=\frac{4}{3}\)
=> AE = \(\frac{4.1,5}{3}=2\left(cm\right)\)
Xét ΔABC có DE//BC (gt) => \(\frac{AD}{AB}=\frac{DE}{BC}\) (hệ quả đ/lí Ta-lét)
=> DE = \(\frac{AD.BC}{AB}=\frac{4.8}{11}=\frac{32}{11}\left(cm\right)\)
3.
a) Xét ΔOCD có AB//CD (gt), theo đ/lí Ta-lét có: \(\frac{OC}{OA}=\frac{OD}{OB}\)
=> OA.OD = OB.OC
b) Do \(\frac{OC}{OA}=\frac{OD}{OB}\)(cmt) => \(\frac{OC}{OA+OC}=\frac{OD}{OB+OD}\Rightarrow\frac{OC}{AC}=\frac{OD}{BD}\) (1)
Do MN//AB => OM//AB; ON//AB
Xét ΔABD có OM//AB (cmt) => \(\frac{OM}{AB}=\frac{OD}{BD}\) (hệ quả đ/lí Ta-lét) (2)
Xét ΔABC có ON//AB (cmt) => \(\frac{ON}{AB}=\frac{OC}{AC}\) (hệ quả đ/lí Ta-lét) (3)
Từ (1), (2), (3) => \(\frac{OM}{AB}=\frac{ON}{AB}\) => OM = ON

a) Ta có DB = AB - AD = 11 - 4 = 7(cm)
xét tam giác ABC có DE // BC
=> \(\frac{AE}{EC}\) = \(\frac{AD}{BD}\) (định lí ta lét)
=> \(\frac{AE}{EC}\) = \(\frac{4}{7}\)
b) Ta có AE/EC = \(\frac{4}{7}\)
=> AE = \(\frac{4EC}{7}\)
Mà EC - AE = 1,5 nên EC - \(\frac{4EC}{7}\) = 1,5
=> \(\frac{3EC}{7}\) = 1,5
=> EC = 3,5(cm)
=> AE =\(\frac{4EC}{7}\) = \(\frac{4.3,5}{7}\) = 2(cm)
=> AC = AE + EC = 2 + 3,5 = 5,5(cm)

a: BD=10-6=4cm
Xét ΔABC có DE//BC
nên AD/DB=AE/EC
=>AE/EC=3/2
b: AE/EC=3/2
=>2AE-3EC=0
mà AE-EC=3
nên AE=9cm; EC=6cm
=>AC=15cm

Xét \(\Delta ABC\)có: \(DE//BC\)\(\Rightarrow\frac{BD}{AB}=\frac{CE}{AC}\)( hệ quả của định lý Ta lét )
mà \(DB=1,5cm\); \(AB=5cm\)
\(\Rightarrow\frac{CE}{AC}=\frac{1,5}{5}=\frac{3}{10}\)\(\Rightarrow CE=\frac{3}{10}.AC\)
mà \(AC+EC=13\)\(\Rightarrow AC+\frac{3}{10}.AC=13\)
\(\Rightarrow\frac{13}{10}.AC=13\)\(\Rightarrow AC=10\left(cm\right)\)
\(\Rightarrow EC=10.\frac{3}{10}=3\left(cm\right)\)\(\Rightarrow AE=AC-EC=10-3=7\left(cm\right)\)
Vậy \(AC=10cm\); \(EC=3cm\); \(AE=7cm\)
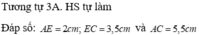

link nek:https://hoidap247.com/cau-hoi/192036~~~ ✔
✔