Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

theo dề bài ta có
AH Là dường cao của tam giác ABC
=>tam giác AHB và tam giác AHC vuông tại H
Xét tam giác ABC cân tại A ta có
AH Là dường cao kẻ từ dỉnh A
=>AH cũng là dường trung tuyến ứng cạnh BC
=> BH=HC
xét tam giác AHB (góc H =90 dộ )và tam giác AHC (góc H =90 dộ )
AB=AC(do tam giác ABC cân tại A
BH=HC(chứng minh trên)
=>tam giác AHB=tam giác AHC (cạnh huyền- cạnh góc vuông)
C2
theo dề bài ta có
AH vuông góc vs BC
=>Ah là dường cao cua tam giác ABc
=>tam giác AHB và tam giác AHc vuông tại h
xét tam giác AHB (H =90 độ)và tam giác AHC (h=90 dộ )
AH là cạnh chung
BH=HC(chứng minh như trên )
=>Tam giác AHB=tam giác AHC (hai cạnh góc vuông )

theo đề bài ta có
AH Là dường cao của tam giác ABC
=>tam giác AHB và tam giác AHC vuông tại H
Xét tam giác ABC cân tại A ta có
AH Là dường cao kẻ từ dỉnh A
=>AH cũng là dường trung tuyến ứng cạnh BC
=> BH=HC
xét tam giác AHB (góc H =90 dộ )và tam giác AHC (góc H =90 dộ )
AB=AC(do tam giác ABC cân tại A
BH=HC(chứng minh trên)
=>tam giác AHB=tam giác AHC (cạnh huyền- cạnh góc vuông)
C2 theo dề bài ta có
AH vuông góc vs BC
=>Ah là dường cao cua tam giác ABc
=>tam giác AHB và tam giác AHc vuông tại h
xét tam giác AHB (H =90 độ)và tam giác AHC (h=90 dộ )
AH là cạnh chung
BH=HC(chứng minh như trên )
=>Tam giác AHB=tam giác AHC (hai cạnh góc vuông )

Chứng minh được △ A H B = △ A H C (cạnh huyền - cạnh góc vuông)

a) Xét \(\Delta ABH\) vuông tại H và \(\Delta ACH\text{vuông tại H}:\)
AB = AC \((\Delta ABC\text{cân tại A}).\)
\(\widehat{B}=\widehat{C}\) \((\Delta ABC\text{cân tại A}).\)
\(\Rightarrow\Delta ABH=\Delta ACH\) (cạnh huyền - góc nhọn).
b) Xét \(\Delta ABC\) cân tại A:
AH là đường cao \(\left(AH\perp BC\right).\)
\(\Rightarrow\) AH là phân giác \(\widehat{BAC}.\)
c) Ta có: BH = CH = \(\dfrac{1}{2}BC=\dfrac{1}{2}8=4\left(cm\right).\)
Xét \(\Delta ABH:\)
\(AB^2=AH^2+BH^2\left(Pytago\right).\\ \Rightarrow AB^2=3^2+4^2.\\ \Rightarrow AB=5\left(cm\right).\)
Mà AB = AC (\(\Delta ABC\) cân tại A).
\(\Rightarrow AC=5\left(cm\right).\)

a: Xét ΔABH vuông tại H và ΔACH vuông tại H có
AB=AC
AH chung
Do đó: ΔABH=ΔACH
b: Xét ΔAMH vuông tại M và ΔANH vuông tại N có
AH chung
\(\widehat{MAH}=\widehat{NAH}\)
Do đó: ΔAMH=ΔANH
Suy ra: AM=AN
hay ΔAMN cân tại A
c: Xét ΔABC có AM/AB=AN/AC
nên MN//BC

@trần thị giang : thì mình KHÔNG hỏi bạn, nếu ai biết thì trả lời, CÂM ĐƯỢC RỒI

`#3107.101107`
`a,`
Xét $\triangle ABH$ và $\triangle ACH$:
`AB = AC` $(\triangle ABC$cân tại A`)`
\(\widehat{B}=\widehat{C}\) $(\triangle ABC$cân tại A`)`
`HB = HC ( H` là trung điểm của BC`)`
$=> \triangle ABH = \triangle ACH (c - g - c)$
Vì $\triangle ABH = \triangle ACH$
`=>`\(\widehat{AHB}=\widehat{AHC}\left(\text{2 góc tương ứng}\right)\)
Mà `2` góc này nằm ở vị trí kề bù
`=>` \(\widehat{AHB}+\widehat{AHC}=180^0\)
`=>` \(\widehat{AHB}=\widehat{AHC}=\dfrac{180^0}{2}=90^0\) `=> AH \bot BC`
`b,`
Vì $\triangle ABH = \triangle ACH (a)$
`=>`\(\widehat{BAH}=\widehat{CAH}\left(\text{2 góc tương ứng}\right)\)
Xét $\triangle AHM$ và $\triangle AHN$:
AH chung
\(\widehat{MAH}=\widehat{NAH}\left(CMT\right)\)
\(\widehat{AMH}=\widehat{ANH}\left(=90^0\right)\)
$=> \triangle AHM = \triangle AHN (ch - gn)$
`c,`
Xét $\triangle HMB$ và $\triangle HNC$:
\(\widehat{HMB}=\widehat{HNC}\left(=90^0\right)\)
`HB = HC` `(`gt`)`
\(\widehat{HBM}=\widehat{HCN}\) $(\triangle ABC$ cân tại A`)`
$=> \triangle HMB = \triangle HNC (ch - gn)$
`=>`\(\widehat{BHM}=\widehat{CHN}\left(2\text{ góc tương ứng}\right)\) `(1)`
Vì \(\left\{{}\begin{matrix}\widehat{MHB}+\widehat{KHB}=\widehat{MHK}\\\widehat{NHC}+\widehat{IHC}=\widehat{NHI}\end{matrix}\right.\)
Mà \(\widehat{MHK}=\widehat{NHI}\left(\text{đối đỉnh}\right)\) `(2)`
Từ `(1)` và `(2)` `=>` \(\widehat{KHB}=\widehat{IHC}\)
Xét $\triangle KHB$ và $\triangle IHC$:
\(\widehat{KBH}=\widehat{ICH}\left(\widehat{ABC}=\widehat{ACB}\right)\)
`HB = HC`
\(\widehat{KHB}=\widehat{IHC}\)
$=> \triangle KHB = \triangle IHC (g - c - g)$
`=> BK = CI` `(2` cạnh tương ứng`)`
Ta có:
`AK = AB + BK`
`AI = AC + CI`
Mà `AB = AC; BK = CI`
$=> AK = AI => \triangle AIK$ cân tại A.
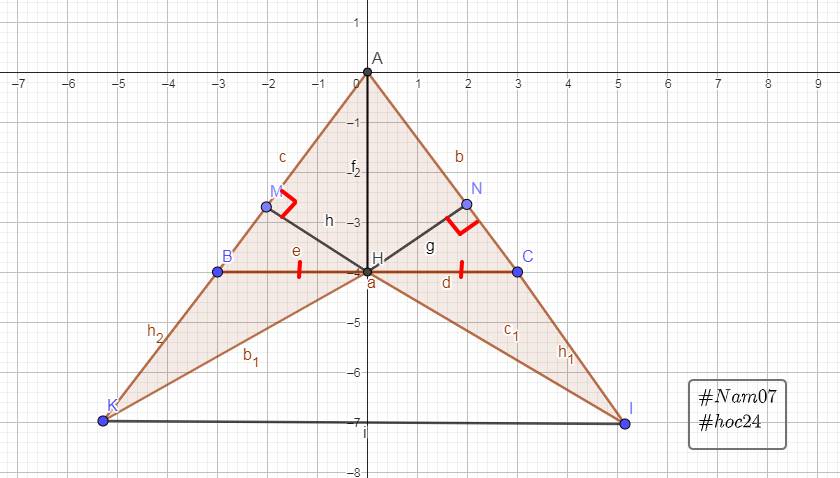

a) Xét ΔABH vuông tại H và ΔACH vuông tại H có
AB=AC(ΔABC cân tại A)
AH chung
Do đó: ΔABH=ΔACH(Cạnh huyền-cạnh góc vuông)
b) Ta có: ΔABH=ΔACH(cmt)
nên BH=CH(hai cạnh tương ứng)
c) Xét ΔHIB vuông tại I và ΔHKC vuông tại K có
HB=HC(cmt)
\(\widehat{B}=\widehat{C}\)(hai góc ở đáy của ΔABC cân tại A)
Do đó: ΔHIB=ΔHKC(cạnh huyền-góc nhọn)
Xét tg ABC cân tại A có: AH là đường cao (gt)
=> \(\left\{{}\begin{matrix}\text{AH là đường phân giác}\\\text{AH là đường trung tuyến}\end{matrix}\right.\)(tc các đường trong tg cân)
Cách 1:
Xét tg AHB và tg AHC có:
AB = AC (tg ABC cân tại A)
^B = ^C (tg ABC cân tại A)
BH = CH ( H là TĐ BC do AH là trung tuyến)
=> tg AHB = tg AHC (cgc)
C 2:
Xét tg AHB và tg AHC có:
AB = AC (tg ABC cân tại A)
AH chung
BH = CH ( H là TĐ BC do AH là trung tuyến)
=> tg AHB = tg AHC (ccc)