Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác AHBE có
M là trung điểm của AB
M là trung điểm của HE
Do đó: AHBE là hình bình hành
mà \(\widehat{AHB}=90^0\)
nên AHBE là hình chữ nhật
b: Xét tứ giác ABFC có
H là trung điểm của AF
H là trung điểm của BC
Do đó:ABFC là hình bình hành
mà AB=AC
nên ABFC là hình thoi
a) Ta có: E đối xứng với H qua M (gt)
=> M là trung điểm của HE
Xét tứ giác AHBE có:
MA = MB (M là trung điểm của AB)
ME = MH (M là trung điểm của HE)
\(\widehat{AHB}=90^o\)(Vì AH là đường cao vuông góc với BC)
=> AHBE là hcn (đpcm)
b, Vì ABC là tam giác cân
=> AB = AC (1)
Vì F đối xứng với A qua H
=> FB = AB ; FC = AC (2)
Từ (1) và (2) => AB = AC = FC = FB
Xét tứ giác ABFC có: AB = AC = FC = FB (cm trên)
=> ABFC là hình thoi (đpcm)

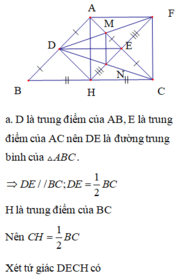
a: Xét ΔABC có
D là trung điểm của AB
E là trung điểm của AC
Do đó: DE là đường trung bình
=>DE//BC và DE=BC/2
hay DE//BF và DE=BF
=>BDEF là hình bình hành
b: Xét tứ giác AMCF có
E là trung điểm của AC
E là trung điểm của MF
Do đó: AMCF là hình bình hành
mà \(\widehat{AMC}=90^0\)
nên AMCF là hình chữ nhật

a: Xét ΔABC có
D là tđiểm của AB
E là tđiểm của AC
Do đó: DE là đường trung bình
=>DE//FC và DE=FC
hay DECF là hình bình hành

Bài 2:
a: Ta có: ΔABC cân tại A
mà AH là đường trung tuyến
nên AH là đường cao
b: Xét tứ giác BHAD có
I là trung điểm của AB
I là trung điểm của HD
Do đó: BHAD là hình bình hành
mà \(\widehat{AHB}=90^0\)
nên BHAD là hình chữ nhật

xét tam giác abc có e là trung điểm của ab (gt)
f là trunng điểm của ac (gt)
=> ef là đường tuẻng bình của tam giác abc(dn....)
=> ef//bc=>efcb là hiình thang
b)có ef là đường trung bình của tam giác abc (cmt)
=> ef=1/2 bc hay ef+ef=bc mà ef=de =>de+ef=bc => df=bc mà df//bc( vì ef//bc cmt)
=> dfcb là hình bình hành (dn...)


a: Xét ΔABC có
E là trung điểm của AB
F là trung điểm của AC
Do đó: EF là đường trung bình của ΔABC
Suy ra: BC=2FE và FE//BC
Xét tứ giác EFCB có EF//BC
nên EFCB là hình thang
mà \(\widehat{C}=\widehat{B}\)
nên EFCB là hình thang cân