Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔABC có
E là trung điểm của AB
D là trung điểm của AC
Do đó: ED là đường trung bình của ΔBAC
Suy ra: ED//BC và \(ED=\dfrac{BC}{2}\left(1\right)\)
Xét ΔGBC có
M là trung điểm của GB
N là trung điểm của GC
Do đó: MN là đường trung bình của ΔGBC
Suy ra: MN//BC và \(MN=\dfrac{BC}{2}\left(2\right)\)
Từ (1) và (2) suy ra ED//MN và ED=MN
hay MNDE là hbh

a: Xét ΔABC có
E là trung điểm của AB
D là trung điểm của AC
Do đó: ED là đường trung bình của ΔBAC
Suy ra: ED//BC và \(ED=\dfrac{BC}{2}\left(1\right)\)
Xét ΔGBC có
M là trung điểm của GB
N là trung điểm của GC
Do đó: MN là đường trung bình của ΔGBC
Suy ra:MN//BC và \(MN=\dfrac{BC}{2}\left(2\right)\)
Từ (1) và (2) suy ra ED//MN và ED=MN
hay MNDE là hình bình hành

a: Xét ΔABC có
E là trung điểm của AB
D là trung điểm của AC
Do đó: ED là đường trung bình của ΔABC
Suy ra: ED//BC và ED=BC/2(1)
Xét ΔGBC có
M là trung điểm của BG
N là trung điểm của CG
Do đó: MN là đường trung bình của ΔGBC
Suy ra: MN//BC và MN=BC/2(2)
Từ (1) và (2) suy ra MN//DE và MN=DE
hay MNDE là hình bình hành

\(a,\) Vì E,D là trung điểm AB,AC nên ED là đường trung bình tam giác ABC
Do đó \(ED//BC;ED=\dfrac{1}{2}BC(1)\)
Vì H,K là trung điểm GB,GC nên HK là đường trung bình tam giác BGC
Do đó \(HK//BC;HK=\dfrac{1}{2}BC(2)\)
Từ \((1)(2)\Rightarrow HK//ED;HK=ED\)
Vậy DEHK là hình bình hành
\(b,\Delta ABC\) cân tại A nên \(AB=AC\Rightarrow \dfrac{1}{2}AB=\dfrac{1}{2}AC\)
\(\Rightarrow AE=EB=AD=DC\)
Ta có \(AB=AC;AE=AD;\widehat{BAC}\) chung
\(\Rightarrow \Delta ADB=\Delta AEC(c.g.c)\\ \Rightarrow BD=EC\)
Lại có G là trọng tâm tam giác ABC nên \(CK=KG=GE=\dfrac{1}{3}CE\)
\(BH=HG=GD=\dfrac{1}{3}BD\)
Do đó \(KG+GE=HG+GD(\dfrac{2}{3}BD=\dfrac{2}{3}CE)\)
\(\Rightarrow EK=HD\)
Vậy DEHK là hình chữ nhật

a: Xét tứ giác DEFH có
DE//FH
DE=FH
Do đó: DEFH là hình bình hành

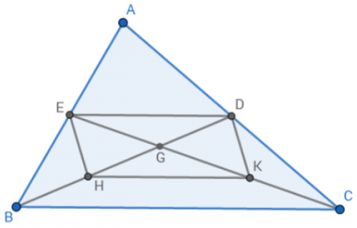
a)
BD là đường trung tuyến của Δ ABC nên D là trung điểm của AC (1)
CE là đường trung tuyến của Δ ABC nên E là trung điểm của AB (2)
Từ (1) và (2) suy ra :
DE là đường trung bình của Δ ABC
=> DE // BC và DE = 1/2 BC
Δ BGC có H là trung điểm của GB và K là trung điểm của GC
suy ra HK là đường trung bình của Δ BGC
=> HK // BC và HK = 1/2 BC
Tứ giác DEHK có DE//BC, HK // BC và DE = HK = 1/2 BC
nên tứ giác
b) DEHK là hình bình hành nên
HG = GD = 1/2 HD và GE = GK = 1/2 EK
Để tứ giác DEHK là hình chữ nhật thì
HD = EK => 1/2 HD = 1/2 EK => GE = GD và GH = GK
GH = GK => 2GH = 2GK => GB = GC
Xét Δ GEB và Δ GDC có
GE = GD Góc EGB = góc DGC GB = GC => ΔGEB = ΔGDC (c.g.c) => BE = CD => 2BE = 2CD => AB = AC => ΔABC cân tại A Vậy đểtứ giác DEHK là hình chữ nhật thì
ΔABC cân tại Ac) BD ⊥ CE => HD ⊥ EK Hình bình hành DEHK có HD ⊥ EK nên DEHK là hình thoi Vậy
nếu các đường trung tuyến BD và CE vuông góc với nhau thì tứ giác DEHK là hình thoi

a: Xét ΔABC có
E là trung điểm của AB
D là trung điểm của AC
DO đó: ED là đường trung bình
=>ED//BC và ED=BC/2(1)
Xét ΔGBC có
I là trung điểm của GB
K là trung điểm của GC
Do đó: IK là đường trung bình
=>IK//BC và IK=BC/2(2)
Từ (1) và (2) suy ra ED//IK và ED=IK
hay EDKI là hình bình hành


a: Xét ΔABC có
E là trung điểm của AB
D là trung điểm của AC
Do đó: ED là đường trung bình của ΔABC
Suy ra: ED//BC và ED=BC/2(1)
Xét ΔGBC có
F là trung điểm của GB
H là trung điểm của GC
Do đó: FH là đường trung bình của ΔGBC
Suy ra: FH//BC và FH=BC/2(2)
Từ (1) và (2) suy ra ED//FH và ED=FH
hay EFHD là hình bình hành