Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: AB<AC<BC
=>góc C<gócB<góc A
b: Xét ΔABD và ΔEBD có
BA=BE
góc ABD=góc EBD
BD chung
=>ΔBAD=ΔBED
c,d: ΔBAD=ΔBED
=>góc ADB=góc EDB và góc BAD=góc BED=90 độ
=>DB là phân giác của góc ADE và DE vuông góc BC

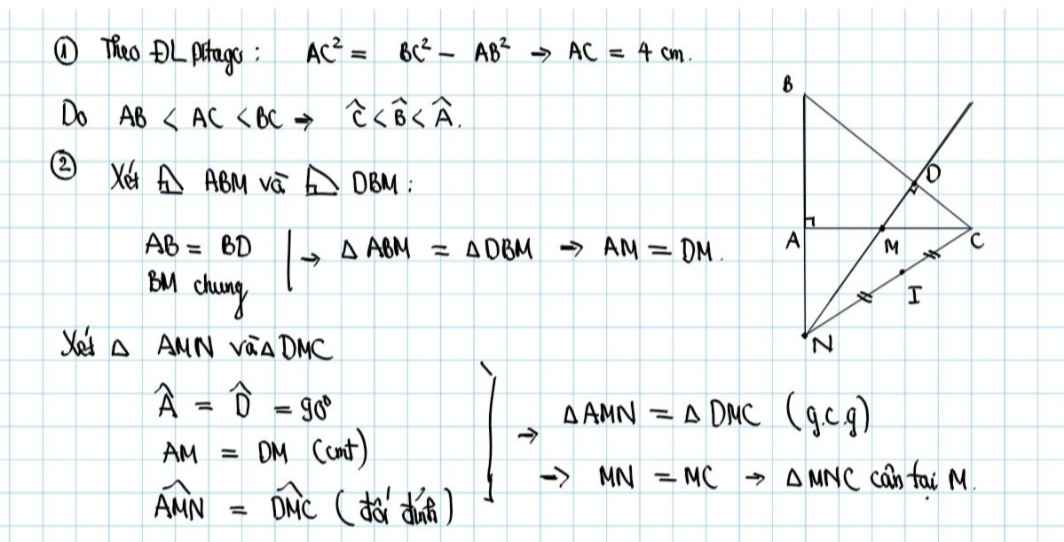
a: AC=căn 5^2-3^2=4cm
AB<AC<BC
=>góc C<góc B<góc A
b: xét ΔBAM vuông tại A và ΔBDM vuông tại D có
BM chung
BA=BD
=>ΔBAM=ΔBDM
=>MA=MD
Xét ΔMAN vuông tại A và ΔMDC vuông tại D có
MA=MD
góc AMN=góc DMC
=>ΔMAN=ΔMDC
=>MN=MC
=>ΔMCN cân tại M

a: \(AC=\sqrt{5^2-3^2}=4\left(cm\right)\)
Xét ΔABC có AB<AC<BC
nên \(\widehat{C}< \widehat{B}< \widehat{A}\)
b: Xét ΔBAM vuông tại A và ΔBDM vuông tại D có
BA=BD
BM chung
Do đó: ΔBAM=ΔBDM
Suy ra: MA=MD
Xét ΔAMN vuông tại A và ΔDMC vuông tại D có
MA=MD
\(\widehat{AMN}=\widehat{DMC}\)
Do đó: ΔAMN=ΔDMC
Suy ra: MN=MC
hay ΔMNC cân tại M

a: Xét ΔABC có AB<BC<AC
nên \(\widehat{C}< \widehat{A}< \widehat{B}\)
b: XétΔABC có \(AC^2=BA^2+BC^2\)
nên ΔABC vuông tại B
a, Ta có AC > BC > AB
=> ^B > ^A > ^C
b, Ta có \(AC^2=AB^2+BC^2\Leftrightarrow100=64+36\)*đúng*
Vậy tam giác ABC vuông tại B

a: Ta có: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=3^2+4^2=25\)
=>\(BC=\sqrt{25}=5\left(cm\right)\)
Xét ΔABC có AB<AC<BC
mà \(\widehat{C};\widehat{B};\widehat{A}\) lần lượt là góc đối diện của các cạnh AB,AC,BC
nên \(\widehat{ACB}< \widehat{CBA}< \widehat{BAC}\)
b: Xét ΔABD có
AH là đường cao
AH là đường trung tuyến
Do đó: ΔABD cân tại A

bài 2:
ta có: AB<AC<BC(Vì 3cm<4cm<5cm)
=> góc C>góc A> góc B (Các cạnh và góc đồi diện trong tam giác)
Bài 3:
*Xét tam giác ABC, có:
góc A+góc B+góc c= 180 độ( tổng 3 góc 1 tam giác)
hay góc A+60 độ +40 độ=180độ
=> góc A= 180 độ-60 độ-40 độ.
=> góc A=80 độ
Ta có: góc A>góc B>góc C(vì 80 độ>60 độ>40 độ)
=> BC>AC>AB( Các cạnh và góc đối diện trong tam giác)
bài 2:
ta có: AB <AC <BC (Vì 3cm <4cm <5cm)
=> góc C>góc A> góc B (Các cạnh và góc đồi diện trong tam giác)
Bài 3:
*Xét tam giác ABC, có:
góc A+góc B+góc c= 180 độ( tổng 3 góc 1 tam giác)
hay góc A+60 độ +40 độ=180độ
=> góc A= 180 độ-60 độ-40 độ.
=> góc A=80 độ
Ta có: góc A>góc B>góc C(vì 80 độ>60 độ>40 độ)
=> BC>AC>AB( Các cạnh và góc đối diện trong tam giác)
HT mik làm giống bạn Dương Mạnh Quyết

a) Xét tam giác ABC có:
BC>AC>AB (vì 5>4>3)
Suy ra: Góc A>góc B>góc C (quan hệ giữa góc và cạnh đối diện)
b) Xét tam giác BCD có:
A là trung điểm của BD (gt)
I là trung điểm của BC(gt)
A cắt I tại M
Suy ra M là trọng tâm của tâm giác CBD (Tính chất)
a) Xét tam giác ABC có:
BC>AC>AB (vì 5>4>3)
Suy ra: Góc A>góc B>góc C (quan hệ giữa góc và cạnh đối diện)
b) Xét tam giác BCD có:
A là trung điểm của BD (gt)
I là trung điểm của BC(gt)
A cắt I tại M
Suy ra M là trọng tâm của tâm giác CBD (Tính chất)

a: Xét ΔABC có AB<AC<BC
mà \(\widehat{C};\widehat{B};\widehat{A}\) lần lượt là góc đối diện của các cạnh AB,AC,BC
nên \(\widehat{C}< \widehat{B}< \widehat{A}\)
b: Vì \(\widehat{C}< \widehat{B}< \widehat{A}\)
nên \(\widehat{A}\) là góc lớn nhất trong ΔABC