
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


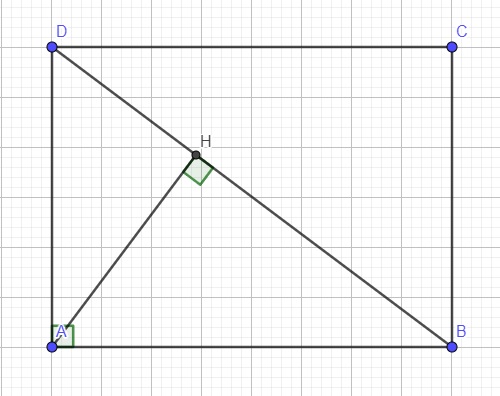
a.
Do ABCD là hình chữ nhật \(\Rightarrow\widehat{HBA}=\widehat{CDB}\) (so le trong)
Xét hai tam giác HBA và CDB có:
\(\left\{{}\begin{matrix}\widehat{HBA}=\widehat{CDB}\left(cmt\right)\\\widehat{AHB}=\widehat{BCD}=90^0\end{matrix}\right.\) \(\Rightarrow\Delta HBA\sim\Delta CDB\left(g.g\right)\)
b.
Xét hai tam giác AHD và BAD có:
\(\left\{{}\begin{matrix}\widehat{ADB}\text{ chung}\\\widehat{AHD}=\widehat{BAD}=90^0\end{matrix}\right.\) \(\Rightarrow\Delta AHD\sim\Delta BAD\left(g.g\right)\)
\(\Rightarrow\dfrac{AD}{DB}=\dfrac{DH}{AD}\Rightarrow AD^2=DH.DB\)
c.
Áp dụng định lý Pitago cho tam giác vuông BAD:
\(DB=\sqrt{AD^2+AB^2}=\sqrt{BC^2+AB^2}=\sqrt{6^2+8^2}=10\left(cm\right)\)
Theo chứng minh câu b:
\(AD^2=DH.DB\Rightarrow DH=\dfrac{AD^2}{DB}=\dfrac{BC^2}{DB}=\dfrac{6^2}{10}=3,6\left(cm\right)\)
Áp dụng Pitago cho tam giác vuông AHD:
\(AH=\sqrt{AD^2-HD^2}=\sqrt{6^2-3,6^2}=4,8\left(cm\right)\)

a) Đặt \(A=4x-x^2-5\)
\(-A=x^2-4x+5\)
\(-A=\left(x^2-4x+4\right)+1\)
\(-A=\left(x-2\right)^2+1\)
Mà \(\left(x-2\right)^2\ge0\forall x\)
\(\Rightarrow-A\ge1\)
\(\Leftrightarrow A\le-1< 0\left(đpcm\right)\)
b) Đặt \(B=x^2-2x+5\)
\(B=\left(x^2-2x+1\right)+4\)
\(B=\left(x-1\right)^2+4\)
Mà \(\left(x-1\right)^2\ge0\forall x\)
\(\Rightarrow B\ge4>0\left(đpcm\right)\)
a)4x-x2-5 = -(x2-4x+4)-1= -(x-2)^2 -1 < 0 với mọi x (đpcm)
b) x2 -2x+5= (x2-2x+1)+4=(x-1)^2 +4 >0 với mọi x (đpcm)

2a^2 +2b^2 -5ab = 0
2a^2 -4ab -ab +2b^2 = 0
2a(a-2b) -b(a-2b) = 0
(2a-b)(a-2b) = 0
Suy ra: 2a=b hoặc a=2b
Mà a>b>0 nên a=2b
Ta có: P = a+b/a-b = 2b+b/ 2b-b = 3b/b=3
Vậy P = 3
Chúc bạn học tốt.
Ta có: \(2a^2+2b^2=5ab\)
\(\Leftrightarrow2a^2+2b^2-5ab=0\)
\(\Leftrightarrow2a^2-4ab-ab+2b^2=0\)
\(\Leftrightarrow2a\left(a-2b\right)-b\left(a-2b\right)=0\)
\(\Leftrightarrow\left(a-2b\right)\left(2a-b\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}a-2b=0\\2a-b=0\end{cases}\Leftrightarrow\orbr{\begin{cases}a=2b\\2a=b\end{cases}}}\)
Mà a > b > 0 nên a = 2b
Thế vào, ta được: \(P=\frac{a+b}{a-b}=\frac{2b+b}{2b-b}=\frac{3b}{b}=3\)
Vậy P = 3

\(VT=\dfrac{a^2}{b+ab^2c}+\dfrac{b^2}{b+abc^2}+\dfrac{c^2}{c+a^2bc}\ge\dfrac{\left(a+b+c\right)^2}{a+b+c+abc\left(a+b+c\right)}=\dfrac{9}{3+3abc}\)
\(VT\ge\dfrac{9}{3+\dfrac{\left(a+b+c\right)^3}{9}}=\dfrac{3}{2}\)
Dấu "=" xảy ra khi \(a=b=c=1\)

Ta có: \(\frac{a^2}{b}+\frac{b^2}{a}+7\left(a+b\right)\ge8\sqrt{2\left(a^2+b^2\right)}\)
\(\Leftrightarrow a^3+b^3+7ab\left(a+b\right)\ge8ab\sqrt{2\left(a^2+b^2\right)}\)
Ta có: \(VP=8\sqrt{ab}\sqrt{\left(a^2+b^2\right)\cdot2ab}\le^{am-gm}4\sqrt{ab}\left(a+b\right)^2\)
\(VT=\left(a+b\right)\left[\left(a+b\right)^2+4ab\right]\ge^{am-gm}\left(a+b\right)4\sqrt{ab}\left(a+b\right)\ge VP\)
=> ĐPCM
a < b
=> 2a < 2b (Nhân 2 vào 2 vế của BPT)
=> -2a > -2b (Nhân -1 vào 2 vế của BPT)
=> -2a + (-5) > -2b + (-5) (Cộng -5 vào 2 vế của BPT)
=> -2a - 5 > -2b - 5 (Đpcm).
cảm ơn rất nhiều ạ