Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
\(\overrightarrow{BC}=\left(-6;-3\right)\)
Trọng tâm của ΔABC là G(2; 1)
Khi tịnh tiến ΔABC thành ΔA'B'C' theo \(\overrightarrow{BC}=\left(-6;-3\right)\) thì G(2;1) cũng sẽ được tịnh tiến theo \(\overrightarrow{BC}=\left(-6;-3\right)\) thành G' (x;y)
⇒ \(\overrightarrow{GG'}=\overrightarrow{BC}\) = (-6 ; -3)
⇒ \(\left\{{}\begin{matrix}x-2=-6\\y-1=-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-4\\y=-2\end{matrix}\right.\). Vậy G' (-4 ; -2)
+ Ta có :
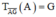
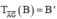với B’ là điểm thỏa mãn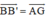 
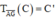với C’ là điểm thỏa mãn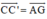 
Vậy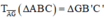 
(hình vẽ).
+ 
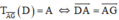⇔ D đối xứng với G qua A (hình vẽ).
Theo công thức trọng tâm\(\Rightarrow G\left(-1;3\right)\)
\(\overrightarrow{u}=\overrightarrow{AG}=\left(-4;3\right)\)
\(\Rightarrow\left\{{}\begin{matrix}x_{G'}=x_G-4=-5\\y_{G'}=y_G+3=6\end{matrix}\right.\)
\(\Rightarrow G'\left(-5;6\right)\)
(Hay G chính là trung điểm của AG')
Phép tịnh tiến bảo toàn diện tích, độ dài, góc, thứ tự điểm, phương của đường thẳng...
Đáp án D
Phát biểuđúng: a , c, e, f, g, i, j, l
b. Phép biến hình biến đường tròn thành đường tròn có bán kính bằng nó có thể là phép tịnh tiến
d. Phép tịnh tiến biến đường tròn thành đường tròn có cùng bán kính
h. Với bất kì 2 điểm A, B và ảnh A’, B’ của chúng qua 1 phép dời hình, ta luôn có AB = A’B’.
k. Nếu phép dời hình biến điểm A thành điểm B thì nó cũng biến điểm B thành A (phát biểu không đúng với phép tịnh tiến)
Gọi phép dời hình đó là f. Do f biến các đoạn thẳng AB, AC tương ứng thành các đoạn thẳng A'B', A'C' nên nó cũng biến các trung điểm M, N của các đoạn thẳng AB, AC tương ứng theo thứ tự thành các trung điểm M', N' của các đoạn thẳng A'B', A'C'. Vậy f biến các trung tuyến CM, BN của tam giác ABC tương ứng thành các trung tuyến C'M', B'N' của tam giác A'B'C'. Từ đó suy ra f biến trọng tâm G của tam giác ABC của CM và BN thành trọng tâm G' của tam giác A'B'C' là giao của C'M' và B'N'.
Gọi phép dời hình đó là f. Do f biến các đoạn thẳng AB, AC tương ứng thành các đoạn thẳng A'B', A'C' nên nó cũng biến các trung điểm M, N của các đoạn thẳng AB, AC tương ứng theo thứ tự thành các trung điểm M', N' của các đoạn thẳng A'B', A'C'. Vậy f biến các trung tuyến CM, BN của tam giác ABC tương ứng thành các trung tuyến C'M', B'N' của tam giác A'B'C'. Từ đó suy ra f biến trọng tâm G của tam giác ABC của CM và BN thành trọng tâm G' của tam giác A'B'C' là giao của C'M' và B'N'.
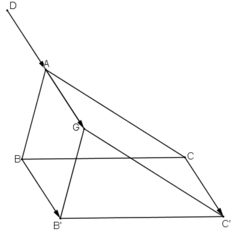
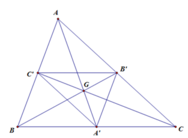
- Dựng hình bình hành ABB'G và ACC'G. Khi đó ta có: \(\overrightarrow{AG}=\overrightarrow{BB'}=\overrightarrow{CC'}\)
. Suy ra \(^T\overrightarrow{AG}\left(A\right)=G,^T\overrightarrow{AG}\left(B\right)=B',^T\overrightarrow{AG}\left(C\right)=C'\)
Do đó ảnh của tam giác ABC qua phép tịnh tiến theo vectơ \(\overrightarrow{AG}\) là tam giác GB'C'.
- Trên tia GA lấy điểm D sao cho A là trung điểm của GD. Khi đó ta có \(\overrightarrow{DA}=\overrightarrow{AG}\). Do đó, \(^T\overrightarrow{AG}\left(D\right)=A\).
- Dựng hình bình hành ABB'G và ACC'G. Khi đó ta có: −−→AG=−−→BB′=−−→CC′AG→=BB′→=CC′→
. Suy ra T−−→AG(A)=G,T−−→AG(B)=B′,T−−→AG(C)=C′TAG→(A)=G,TAG→(B)=B′,TAG→(C)=C′
Do đó ảnh của tam giác ABC qua phép tịnh tiến theo vectơ −−→AGAG→ là tam giác GB'C'.
- Trên tia GA lấy điểm D sao cho A là trung điểm của GD. Khi đó ta có −−→DA=−−→AGDA→=AG→. Do đó, T−−→AG(D)=ATAG→(D)=A.
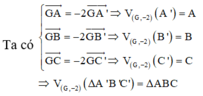
Gọi G là trọng tâm ABC \(\Rightarrow G\left(-1;3\right)\)
\(T_{\overrightarrow{v}}\left(G\right)=G'\Rightarrow\left\{{}\begin{matrix}x'=-1+1=0\\y'=3+4=7\end{matrix}\right.\)
\(\Rightarrow G'\left(0;7\right)\)