SL
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
19 tháng 8 2023
a: \(3\sqrt{200}=3\cdot10\sqrt{2}=30\sqrt{2}\)
b: \(-5\sqrt{50a^2b^2}=-5\cdot5\sqrt{2a^2b^2}\)
\(=-25\cdot\left|ab\right|\cdot\sqrt{5}\)
c: \(-\sqrt{75a^2b^3}\)
\(=-\sqrt{25a^2b^2\cdot3b}=-5\left|ab\right|\cdot\sqrt{3b}\)
17 tháng 8 2023
a: \(A=sin^210^0+sin^280^0+cos^220^0+sin^270^0\)
\(=sin^210^0+cos^210^0+sin^270^0+sin^270^0\)
\(=2\cdot sin^270^0+1\)
b: \(=sin^215^0+sin^275^0+sin^235^0+sin^255^0\)
\(=sin^215^0+cos^215^0+sin^235^0+cos^235^0\)
=1+1
=2
18 tháng 8 2023
\(A=sin^210^0+sin^280^0+cos^220^0+sin^270^0\)
\(=sin^210^0+cos^210^0+sin^270^0+sin^270^0\)
\(=2sin^270^0+1\)
\(B=sin^215^0+sin^275^0+sin^235^0+sin^255^0\)
\(=sin^215^0+cos^215^0+sin^235^0+cos^235^0\)
=1+1
=2
TM
2
H9
HT.Phong (9A5)
CTVHS
26 tháng 8 2023
\(A=2^1+2^2+2^3+...+2^{10}\)
\(\Rightarrow2A=2\cdot\left(2+2^2+2^3+...+2^{10}\right)\)
\(\Rightarrow2A=2^2+2^3+...+2^{11}\)
\(\Rightarrow2A-A=\left(2^2+2^3+...+2^{11}\right)-\left(2+2^2+...2^{10}\right)\)
\(\Rightarrow A=2^{11}-2\)
\(B=3^1+3^2+...+3^{100}\)
\(\Rightarrow3B=3\cdot\left(3+3^2+...+3^{100}\right)\)
\(\Rightarrow3B=3^2+3^3+...+3^{101}\)
\(\Rightarrow3B-B=\left(3^2+3^3+...+3^{101}\right)-\left(3+3^2+3^3+...+3^{100}\right)\)
\(\Rightarrow2B=3^{101}-3\)
\(\Rightarrow B=\dfrac{3^{101}-3}{2}\)
NT
2
H9
HT.Phong (9A5)
CTVHS
17 tháng 8 2023
\(A=sin^210^o+cos^220^o+sin^280^o+cos^270^o\)
\(A=\left(sin^210^o+sin^280^o\right)+\left(cos^220^o+cos^270^o\right)\)
\(A=0+0\)
\(A=0\)
TM
1
ND
Nguyễn Đức Trí
VIP
12 tháng 8 2023
\(A=2+2^2+...2^{2021}\)
\(\Rightarrow A+1=1+2+2^2+...2^{2021}\)
\(\Rightarrow A+1=\dfrac{2^{2021+1}-1}{2-1}\)
\(\Rightarrow A+1=2^{2022}-1\)
\(\Rightarrow A=2^{2022}-2< 2^{2022}=B\)
\(\Rightarrow A< B\)
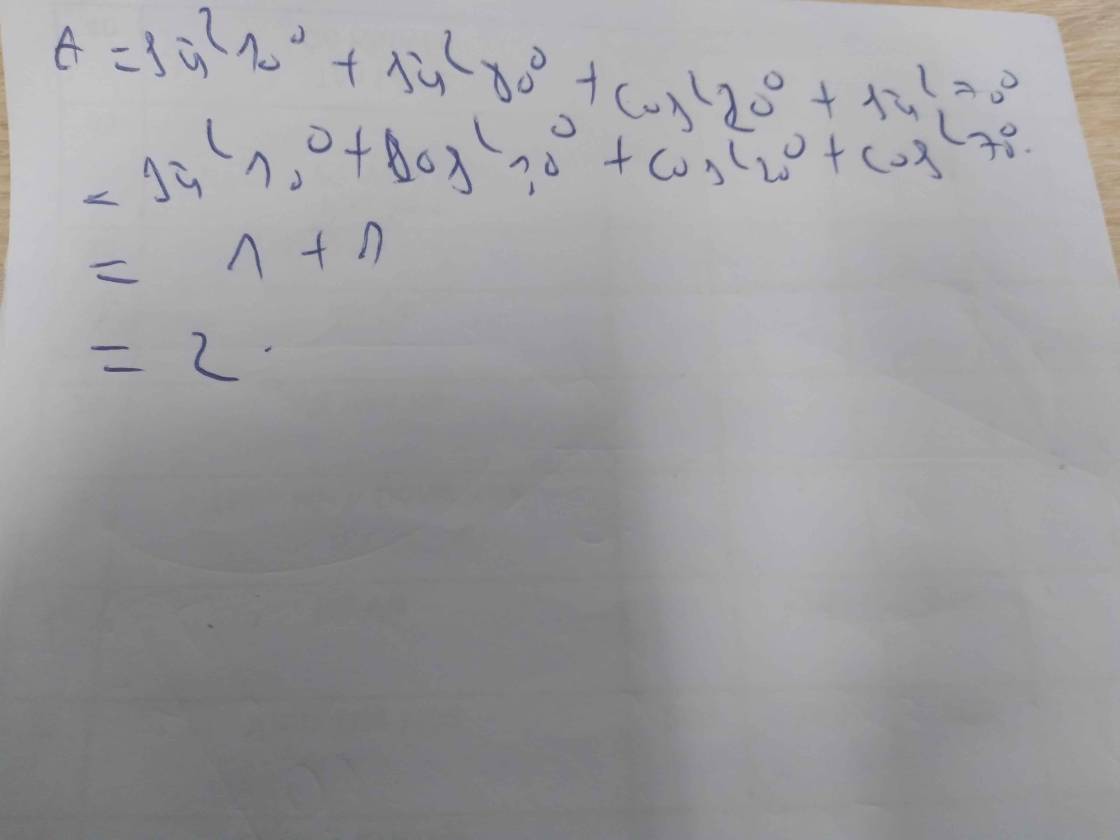
a = 20042 + 20032 + 2002 - 20012
= ....6 + ..9 + ....0 -.... 1 = ....14 => Chữ số hàng chục là 1 (lẻ)
Khi a là SCP có chữ số tận cùng là 4 thì chữ số hàng chục phải là số chẵn
Vì vậy a không phải là SCP (đpcm)