Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a.
AB là đường kính nên \(\widehat{AMB}\) là góc nt chắn nửa đường tròn
\(\Rightarrow\widehat{AMB}=90^0\)
\(\Rightarrow M\) và O cùng nhìn BP dưới 1 góc vuông nên tứ giác OBMP nội tiếp
Mà \(PO=PM\Rightarrow\widehat{PBO}=\widehat{PBM}\)
\(\Rightarrow\Delta_VPBO=\Delta_VPBM\left(ch-gn\right)\) (có cạnh huyền PB chung)
\(\Rightarrow BM=OB=R\)
Vậy M nằm ở vị trí sao cho \(BM=R\) thì \(PO=PM\)
Áp dụng Pitago: \(AM=\sqrt{AB^2-BM^2}=\sqrt{\left(2R\right)^2-R^2}=R\sqrt{3}\)
\(\Rightarrow S_{ABM}=\dfrac{1}{2}AM.BM=\dfrac{R^2\sqrt{3}}{2}\)
b.
\(MB=MP\Rightarrow\Delta MBP\) vuông cân tại M
\(\Rightarrow\widehat{BPM}=45^0\)
Theo câu a ta có OBMP nội tiếp \(\Rightarrow\widehat{BOM}=\widehat{BPM}=45^0\) (cùng chắn BM)
\(\Rightarrow\widehat{BOM}=\dfrac{1}{2}\widehat{BOC}\) \(\Rightarrow M\) là điểm chính giữa cung BC
Khi đó kẻ \(MH\perp AB\Rightarrow\Delta MOH\) vuông cân tại H (tam giác cân có góc đáy bằng 45 độ)
\(\Rightarrow MH=\dfrac{OM}{\sqrt{2}}=\dfrac{R\sqrt{2}}{2}\)
\(S_{AMB}=\dfrac{1}{2}MH.AB=R^2\sqrt{2}\)
c.
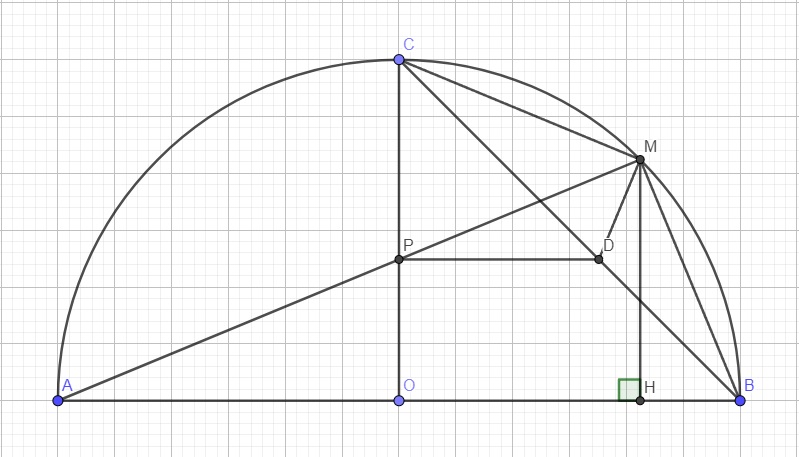
Qua P kẻ đường thẳng song song AB cắt BC tại D
\(\Rightarrow DP\perp CP\Rightarrow\Delta CPD\) nội tiếp đường tròn đường kính CD (1)
\(\widehat{MPD}=\widehat{MAB}\) (đồng vị), mà \(\widehat{MAB}=\widehat{MCB}\) (cùng chắn BM)
\(\Rightarrow\widehat{MPD}=\widehat{MCB}\)
\(\Rightarrow\) Tứ giác MCPD nội tiếp (2 góc bằng nhau cùng chắn MD) (2)
(1);(2) \(\Rightarrow\) M,C,P cùng thuộc đường tròn đường kính CD
Hay tâm I của tam giác CPM nằm trên đường thẳng BC khi M di động trên cung BC

a: Xét (O) có
MA,MB là tiếp tuyến
Do đó: MA=MB
=>ΔMAB cân tại M
b: Xét tứ giác OAMB có
\(\widehat{OAM}+\widehat{OBM}+\widehat{AMB}+\widehat{AOB}=360^0\)
=>\(\widehat{AOB}+60^0+90^0+90^0=360^0\)
=>\(\widehat{AOB}+240^0=360^0\)
=>\(\widehat{AOB}=120^0\)
c: ta có: MA=MB
=>M nằm trên đường trung trực của AB(1)
Ta có: OA=OB
=>O nằm trên đường trung trực của AB(2)
Từ (1) và (2) suy ra MO là đường trung trực của AB
=>MO\(\perp\)AB

Bài 1:
a: Xét (O) có
MA là tiếp tuyến
MB là tiếp tuyến
Do đó: MA=MB
hay ΔMAB cân tại M
mà \(\widehat{AMB}=60^0\)
nên ΔMBA đều
b: Xét ΔAOM vuông tại A có
\(AM=OA\cdot\tan30^0\)
nên \(AM=5\sqrt{3}\left(cm\right)\)
\(C_{AMB}=3\cdot AM=15\sqrt{3}\left(cm\right)\)
c: Ta có: MA=MB
nên M nằm trên đường trung trực của AB(1)
Ta có: OA=OB
nên O nằm trên đường trung trực của AB(2)
Từ (1) và (2) suy ra MO là đường trung trực của AB
hay MO⊥AB(1)
Xét (O) có
ΔABC nội tiếp
AC là đường kính
DO đó: ΔABC vuông tại B
Suy ra: AB⊥BC(2)
Từ (1) và (2) suy ra OM//BC
hay BMOC là hình thang

c
Gọi H là giao điểm của AB và OM
a, Xét Δv MAO và ΔvMBO
Có MO chung
AO=OB(=bk)
=> ΔvMAO= ΔMBO (ch-cgv)
=> MA=MB
Trong ΔAMB
Có MA=MB(cmt)
=> ΔAMB cân tại M
lại có góc AMB=60 độ
=> ΔAMB là Δ đều
b, Ta có: góc AMO=góc BMO ( ΔvMAO= ΔvMBO)
mà góc AMO+ góc BMO= góc AMB=60 độ
=> góc AMO=\(\frac{1}{2}.60=30^0\)
Áp dụng tỉ số lượng giác
Ta có : tan góc AMO=\(\frac{AO}{AM}\)
tan30=\(\frac{5}{AM}\)
=>AM=\(\frac{5}{tan30}=5\sqrt{3}\)
Chu vi ΔAMB= AM.3=\(5\sqrt{3}.3=15\sqrt{3}\)
c, Ta có OA=OB (=bk)
=> O thuộc đường trung trực AB(1)
MA=MB(cmt)
=> M thuộc đường trung trực AB (2)
Từ (1)(2)=> OM là cả đường trung trực
=> MO vuông góc AB (*)
Ta có: OA=OB=OC(=bk)
=> OB=\(\frac{1}{2}AC\)
mà OB là đường trung tuyến
=> Δ ABC vuông tại B
=> AB vuông góc BC(**)
Từ (*)(**)=> MO//BC
=> BMOC là hình thang
Bài 2:
a,
Ta có : góc AQM=90 độ ( MQ vuông góc xy)
góc APM =90 độ ( MP vuông góc AB)
góc QAP=90độ ( xy vuông góc OA)
=> QMPA là hình chữ nhật
b, Trong hình chữ nhật QMPA:
Có : I là trung điểm của đường chéo thứ nhất QP
-> I cũng là trung điểm của đường chéo thứ 2 AM
=> IA=IM
=> OI vuông góc AM tại I ( đường kính đi qua trung điểm => vuông góc ( đ/Lý 3)

a, thay \(x=1,y=2\) vào (d) (\(m\ne\dfrac{2}{3}\))
\(=>\left(3m-2\right).1+m-1=2< =>m=1,25\left(tm\right)\)
b, (d) tạo với Ox 1 góc tù \(< =>3m-2< 0< =>m< \dfrac{2}{3}\)
c,\(=>x=y=0\)
\(=>m-1=0< =>m=1\)


Gọi \(AE\) là đường cao của \(\Delta ABC\)và CD∩AE=F
\(\Delta CBH\) có E,M lần lượt là trung điểm \(CB,CH\)
\(\Rightarrow EM//BH\)
\(\Rightarrow EM\perp DC\)
Áp dụng định lí Menelaus cho tam giác ABE với cát tuyến CFD ta được:
\(\frac{AD}{BD}.\frac{BC}{EC}.\frac{EF}{AF}=1\)
\(\Leftrightarrow FA=FE\)
\(\Delta CEF\)vuông tại \(E\) có đường cao \(EM\)
\(\Rightarrow\hept{\begin{cases}\widehat{MFE}=\widehat{MEC}\Rightarrow\widehat{MFA}=\widehat{MEB}\\\frac{ME}{MF}=\frac{EC}{EF}=\frac{EB}{FA}\end{cases}}\)
\(\Delta MEB\)và \(\Delta MFA\)có:
\(\hept{\begin{cases}\widehat{MFA}=\widehat{MEB\left(cmt\right)}\\\frac{ME}{MF}=\frac{EB}{FA}\left(cmt\right)\end{cases}}\)
\(\Rightarrow\Delta MEB\)đồng dạng \(\Delta MFA\)
\(\Rightarrow\widehat{FMA}=\widehat{EMA}\)
\(\widehat{AMB}=\widehat{DMB}+\widehat{AMF}=\widehat{DMB}+\widehat{BME}=90^0\)
\(\Rightarrow MB\perp MA\)
hay \(\widehat{ANB}=90^0\left(ĐPCM\right)\)