Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hàm số đơn điệu trên đoạn nên giá trị nhỏ nhất – lớn nhất sẽ đạt tại đầu mút của đoạn
Ta có f’ (x) = -x2-1< 0 với a< x< b ; suy ra hàm số y= f( x) là hàm số nghịch biến trên [ a; b].
Mà a< b nên f(a) > f( b)
Vậy m i n [ a ; b ] f ( x ) = f ( b )
Chọn C.

Chọn A
Hàm số y = f(x) thỏa mãn f'(x) < 0 ∀ x ∈ ( a ; b ) nên hàm số nghịch biến trên (a;b).
Do đó ![]()

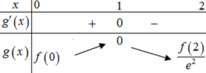
Ta có bảng biến thiên như hình vẽ sau:
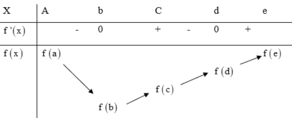
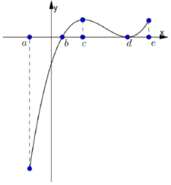
Giá trị nhỏ nhất của hàm số là f( b) nhưng giá trị lớn nhất có thể là f (a) hoặc f( e) Theo giả thiết ta có: f(a) + f( c)) = f( b) + f( d) nên f(a) - f( d)) = f( b) - f( c)< 0
Suy ra : f( a) < f( d) < f( e)
Vậy m a x [ a ; e ] f ( x ) = f ( e ) ; m i n [ a ; e ] f ( x ) = f ( b )
Chọn C.

Ghi lại đề bài đi bạn, đề thế này không ai biết nó là gì cả
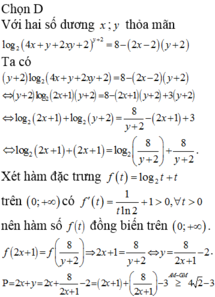
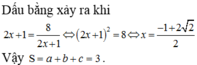
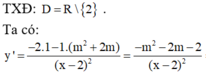
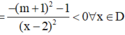
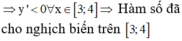
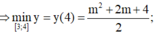
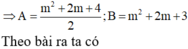

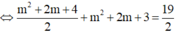
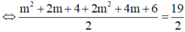
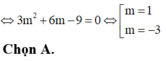






Chọn C