Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(log_xy=log_yx=\frac{1}{log_xy}\Rightarrow\left(log_xy\right)^2=1\Rightarrow\left[{}\begin{matrix}log_xy=1\\log_xy=-1\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=y\\x=\frac{1}{y}\end{matrix}\right.\)
Do \(log_x\left(x-y\right)\) tồn tại \(\Rightarrow x-y\ne0\Rightarrow x\ne y\Rightarrow x=\frac{1}{y}\)
\(log_x\left(x-y\right)=log_y\left(x+1\right)\Leftrightarrow log_x\left(x-\frac{1}{x}\right)=-log_x\left(x+1\right)\)
\(\Leftrightarrow log_x\left[\left(x-\frac{1}{x}\right)\left(x+1\right)\right]=0\Leftrightarrow\left(x-\frac{1}{x}\right)\left(x+1\right)=1\)
\(\Leftrightarrow\left(x^2-1\right)\left(x+1\right)=x\Leftrightarrow x^3+x^2-2x-1=0\)
Pt này nghiệm xấu, đề bài có vấn đề

ĐKXĐ: \(x\ne y\)
\(log_xy=\frac{1}{log_xy}\Leftrightarrow log_x^2y=1\Leftrightarrow\left[{}\begin{matrix}log_xy=1\\log_xy=-1\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=y\left(l\right)\\x=\frac{1}{y}\end{matrix}\right.\)
\(log_x\left(x-\frac{1}{x}\right)=log_{x^{-1}}\left(x+\frac{1}{x}\right)\Leftrightarrow log_x\left(x-\frac{1}{x}\right)=-log_x\left(x+\frac{1}{x}\right)\)
\(\Leftrightarrow log_x\left(x-\frac{1}{x}\right)\left(x+\frac{1}{x}\right)=0\Leftrightarrow\left(x-\frac{1}{x}\right)\left(x+\frac{1}{x}\right)=1\)
\(\Leftrightarrow x^2-\frac{1}{x^2}=1\Leftrightarrow x^4-x^2-1=0\Rightarrow x^2=\frac{1+\sqrt{5}}{2}\Rightarrow y^2=\frac{1}{x^2}=\frac{-1+\sqrt{5}}{2}\)
\(\Rightarrow x^2+xy+y^2=\frac{1+\sqrt{5}}{2}+1+\frac{-1+\sqrt{5}}{2}=\sqrt{5}+1\)

Đáp án D
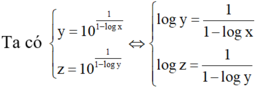
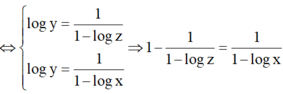
⇔ log z - 1 log z = 1 1 - log x
⇔ 1 - log x = log z log z - 1
⇔ log x = - 1 log z - 1 ⇔ x = 10 1 1 - log z .
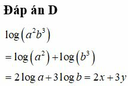
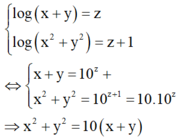


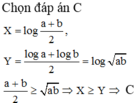
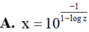
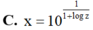
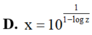
Đáp án A
Phương pháp:
Dựa vào các công thức liên quan đến logarit.
Cách giải:
Khẳng định đúng là: log y x = log a x log a y , với a, b, x, y là các số thực dương khác 1.