Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Ta có
A = log 2017 + log 2016 + log 2015 + log ... + log 3 + log 2 ... > log 2017 + log 2016 > log 2017 + 3 = log 2010 ⇒ A > log 2010
Áp dụng bất đẳng thức log x < x , ∀ x > 1 , ta có
2015 + log 2014 + log ... + log 3 + log 2 ... < 2015 + 2014 + log ... + log 3 + log 2 ... < 2015+1014+2013+ ... +3+2= 2017 × 2014 2
Khi đó
log 2016 + log 2015 + log 2014 + log ... + log 3 + log 2 ... < log 2016 + 2017 × 2014 2 < 4
Vậy A < log 2017 + 4 = log 2021 → A ∈ log 2010 ; 2021

Đáp án D.
Dựa vào đáp án ta suy ra 3 < A < 4 .
⇒ 3 < log 2019 < A 2016 = log 2016 + A 2015 < log 2020 < 4
⇒ 3 < log 2020 < A 2017 = log 2017 + A 2016 < log 2021 < 4
Vậy A 2017 ∈ log 2020 ; log 2021 .

Đáp án D.
Vì M ∈ O x y , M ∈ O x z , P ∈ O y z ⇒ z M = , y N = 0 , z P = 0
Mà M,N,P nằm trên đoạn AB sao cho A M = M N = N P = P B ⇒ A M ¯ = M N ¯ = N P ¯ = P B ¯
Khi đó A B ¯ = 4 A M ¯ ⇒ c - 5 = 4 z M - 5 ⇒ c = - 15 .
Lại có: A B ¯ = 2 A N ¯ ⇒ b + 3 = 2 y N + 3 ⇒ b = 3 .
A B ¯ = 4 P B ¯ ⇒ a - 9 = 4 a + x P ⇒ a = - 3 ⇒ a + b + c = - 15 .

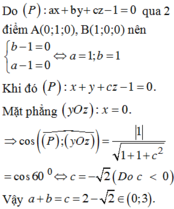

Chọn A.
Phương pháp: Sử dụng định lý Pytago và giải phương trình.
Cách giải: Ta có: