Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

ta có \(\left(log^b_a+log^a_b+2\right)\left(log^b_a-log_{ab}^b\right).log_b^a-1=\left(log^b_a+log^a_b+2\right)\left(log^b_a.log_b^a-log_{ab}^b.log_b^a\right)-1=\left(log^b_a+log^a_b+2\right)\left(1-\frac{1}{log_b^{ba}}log_b^a\right)-1=\left(log^b_a+log^a_b+2\right)\left(1-\frac{1}{1+log^a_b}log^a_b\right)-1=\left(log^b_a+log^a_b+2\right)\frac{1}{1+log^a_b}-1=\left(log^a_b+\frac{1}{log^a_b}+2\right)\frac{1}{1+log^a_b}-1=\frac{\left(1+log^a_b\right)^2}{log^a_b}\frac{1}{1+log^a}-1=\frac{1+log^a_b}{log_b^a}-1=\frac{1}{log_b^a}\)
ta có:
\(\left(log^b_a+\frac{1}{log^b_a}+2\right)\left(log^b_a-\frac{1}{log^{ab}_a}\right)log^a_b-1\)\(=\frac{\left(log^b_a+1\right)^2}{log^b_a}\left(log^b_a-\frac{1}{1+log^b_a}\right)log^a_b-1\)\(=\frac{\left(log^b_a+1\right)^2}{log^b_a}\left(1-\frac{log^a_b}{1+log^b_a}\right)-1\)\(==\frac{\left(log^b_a+1\right)^2}{log^b_a}\left(\frac{1}{1+log^b_a}\right)-1=\frac{1+log^b_a}{log^b_a}-1=\frac{1}{log^b_a}\)

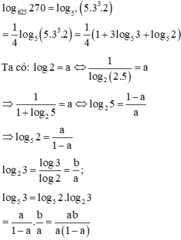
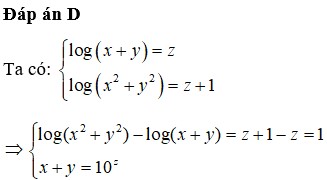
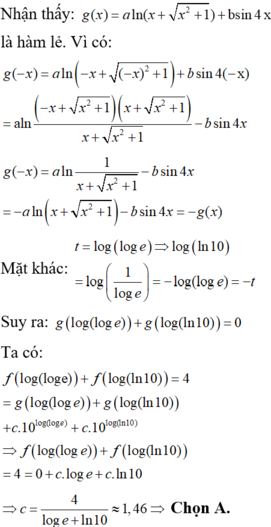
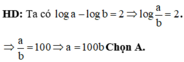


Đáp án A
Sử dụng các công thức biến đổi logarit như: log a b = 1 log b a ; log a b c = log a b + log a c
Cách giải:
Ta có: log a b c 3 = 2 15
⇒ log 3 a b c = 15 2
⇔ log 3 a + log 3 b + log 3 c = 15 2
⇔ 1 log a 3 + 1 log b 3 + log 3 c = 15 2
⇔ log 3 c = 15 2 − 1 log a 3 − 1 log b 3 = 15 2 − 1 2 − 4 = 3
⇔ log 3 c = 1 3 .
Chú ý khi giải: HS thường nhầm lẫn công thức logarit của một tích, hoặc đến bước cuối tính log c 3 lại kết luận nhầm log 3 c = 3 dẫn đến chọn nhầm đáp án.