Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Thay x=4 và y=2 vào y=ax, ta được:
4a=2
hay a=1/2

b: \(\overrightarrow{AB}=\left(6;3\right)\)
\(\overrightarrow{AC}=\left(1;1\right)\)
=>A,B,C ko thẳng hàng
a: Thay x=4 và y=2 vào y=ax, ta được:
4a=2
hay a=1/2

a: I nằm trên trung trực của AC
=>IA=IC
I nằm trên trung trực của BC
=>IB=IC
=>IA=IB
b: Bạn cứ vẽ đường tròn tâm I, bán kính IA là ra ngay á mà

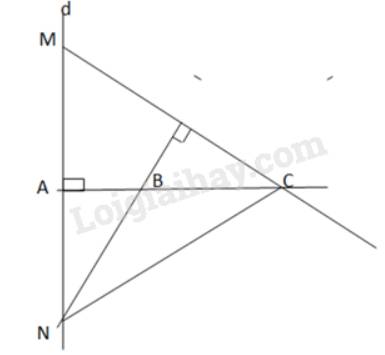
Xét tam giác MNC có 2 đường cao CA và NB cắt nhau tại B
\( \Rightarrow \) B là trực tâm của tam giác MNC
\( \Rightarrow MB \bot CN\)

a) Đồ thị hàm số y = ax đi qua điểm A( 4 ; 2 )
=> A thuộc đồ thị hàm số
=> xA = 4 ; yA = 2
Thế vào đồ thị hàm số ta được :
2 = a . 4 <=> a = 1/2
=> y = 1/2x ( * )
b) Muốn biết ba điểm A, B, C có thẳng hàng hay không , ta xét chúng có cùng đi qua ( * ) hay không
* Xét B( -2 ; -1 )
=> xB = -2 ; yB = -1
Thế vào ( * ) ta được : -1 = 1/2 . ( -2 ) [ đúng ]
Vậy B( -2 ; -1 ) thuộc ( * )
* Xét C( 5 ; 3 )
=> xC = 5 ; yC = 3
Thế vào ( * ) ta được : 3 = 1/2 . 5 [ sai ]
Vậy C(5 ; 3) không thuộc ( * )
=> 3 điểm A, B, C không thẳng hàng
Gọi đường tròn đi qua ba điểm A, B, C có tâm O. Ta có OA = OB = OC.
Ba điểm phân biệt A, B, C không thẳng hàng tạo thành tam giác ABC. Vì OA = OB = OC nên O là giao điểm ba đường trưng trực của tam giác ABC.