Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

-Đặt \(\left\{{}\begin{matrix}b+c-a=x>0\\c+a-b=y>0\\a+b-c=z>0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}2c=x+y\\2a=y+z\\2b=z+x\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}c=\dfrac{x+y}{2}\\a=\dfrac{y+z}{2}\\b=\dfrac{z+x}{2}\end{matrix}\right.\)
\(A=\dfrac{a}{b+c-a}+\dfrac{b}{c+a-b}+\dfrac{c}{a+b-c}=\dfrac{\dfrac{y+z}{2}}{x}+\dfrac{\dfrac{z+x}{2}}{y}+\dfrac{\dfrac{x+y}{2}}{z}=\dfrac{1}{2}\left(\dfrac{y+z}{x}+\dfrac{z+x}{y}+\dfrac{x+y}{z}\right)=\dfrac{1}{2}\left[\left(\dfrac{y}{x}+\dfrac{x}{y}\right)+\left(\dfrac{z}{y}+\dfrac{y}{z}\right)+\left(\dfrac{x}{z}+\dfrac{z}{x}\right)\right]\ge\dfrac{1}{2}.\left(2+2+2\right)=3\left(đpcm\right)\)
-Dấu "=" xảy ra khi \(a=b=c\)

 +
+  +
+  ≥ 3.
≥ 3.
Đặt b + c – a = x > 0 (1); a + c – b = y > 0 (2); a + b – c = z > 0 (3)
Cộng (1) và (2) => b + c – a + a + c – b = x + y ⇔ 2c = x + y ⇔ c = 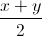
Tương tự a = 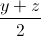 ; b =
; b = 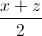
Do đó  +
+  +
+  =
= 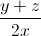 +
+ 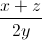 +
+ 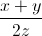 =
=  (
(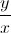 +
+ 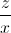 +
+  +
+  +
+ 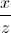 +
+  )
)
=  [(
[(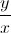 +
+  ) + (
) + (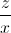 +
+ 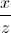 ) + (
) + ( +
+  )] ≥
)] ≥  (2 + 2 + 2) = 3.
(2 + 2 + 2) = 3.
Vậy  +
+  +
+  ≥ 3.
≥ 3.

câu 1 :Đặt b+c-a=x; a+c-b=y ; a+b-c=z
vì a,b,c là 3 cạnh của tam giác nên
b+c-a>0 ; a+c-b>0 ; a+b-c>0
Đặt biểu thức \(\dfrac{a}{b +c-a}\)+\(\dfrac{b}{c+a-b}\)+\(\dfrac{c}{a+b-c}\)=S thì
2S=\(\dfrac{2a}{b+c-a}\)+\(\dfrac{2b}{c+a-b}\)+\(\dfrac{2c}{a+b-c}\)
mà \(\dfrac{2a}{b+c-a}\)=\(\dfrac{a+c-b+a+b-c}{b+c-a}\)=\(\dfrac{y+z}{x}\) , tương tự
\(\dfrac{2b}{c+a-b}\)=\(\dfrac{x+z}{y}\)
\(\dfrac{2c}{a+b-c}\)=\(\dfrac{x+y}{z}\)
=>2S=\(\dfrac{x+y}{z}\)+\(\dfrac{y+z}{x}\)+\(\dfrac{x+z}{y}\)=\(\dfrac{x}{z}\)+\(\dfrac{y}{z}\)+\(\dfrac{y}{x}\)+\(\dfrac{z}{x}\)+\(\dfrac{x}{y}\)+\(\dfrac{z}{y}\)
ta thấy \(\dfrac{x}{z}\)+\(\dfrac{z}{x}\)=\(\dfrac{x^{2^{ }}+z^2}{xz}\)\(\ge\)\(\dfrac{2xz}{xz}\)=2 tương tự với 2 cặp số nghich đảo còn lại thì ta có 2S\(\ge\)2+2+2=6
nên S\(\ge\)3
dấu = xảy ra \(\Leftrightarrow\)x=y=z
câu 2 :
ta có a+b>c ;b+c>a ; a+c>b
xét \(\dfrac{1}{a+c}\)+\(\dfrac{1}{b+c}\)>\(\dfrac{1}{a+b+c}\)+\(\dfrac{1}{b+c+a}\)=\(\dfrac{2}{a+b+c}\)>\(\dfrac{2}{a+b+a+b}\)=\(\dfrac{1}{a+b}\)
tương tự \(\dfrac{1}{a+b}\)+\(\dfrac{1}{a+c}\)>\(\dfrac{1}{b+c}\);\(\dfrac{1}{a+b}\)+\(\dfrac{1}{b+c}\)>\(\dfrac{1}{a+c}\)
nên điều phải chứng minh

a)a,b,c là độ dài 3 cạnh của 1 tam giác
\(\Rightarrow a< b+c\Rightarrow a^2< ab+ac\)
TT\(\Rightarrow b^2< ba+bc\)
\(c^2< ca+cb\)
Cộng vế theo vế ta có đpcm
b)BĐT\(\Leftrightarrow\dfrac{a}{b+c-a}+\dfrac{1}{2}+\dfrac{b}{a+c-b}+\dfrac{1}{2}+\dfrac{c}{a+b-c}+\dfrac{1}{2}\ge\dfrac{9}{2}\)
\(\Leftrightarrow\dfrac{1}{2}\left(\dfrac{a+b+c}{b+c-a}+\dfrac{a+b+c}{a+c-b}+\dfrac{a+b+c}{a+b-c}\right)\ge\dfrac{9}{2}\)
\(\Leftrightarrow\left(a+b+c\right)\left(\dfrac{1}{b+c-a}+\dfrac{1}{c+a-b}+\dfrac{1}{a+b-c}\right)\ge9\)(đúng theo AM-GM)

surf trc khi hỏi Câu hỏi của Duong Thi Nhuong TH Hoa Trach - Phong GD va DT Bo Trach - Toán lớp 8 | Học trực tuyến
Giải:
Ta có BĐT phụ: \(\left(a+b-c\right)\left(b+c-a\right)\left(c+a-b\right)\le abc\)
Áp dụng BĐT Cauchy - Schwarz ta có:
\(\dfrac{a}{b+c-a}+\dfrac{b}{c+a-b}+\dfrac{c}{a+b-c}\)
\(\ge3\sqrt[3]{\dfrac{abc}{\left(b+c-a\right)\left(c+a-b\right)\left(a+b-c\right)}}\)
\(\ge3\sqrt[3]{\dfrac{abc}{abc}}\ge3\) (Đpcm)

đặt b+c-a=x
a+c-b=y
a+b-c=z
ta có x+y=2c
x+z=2b
z+y=2a
ta lại có
2A=\(\dfrac{2a}{x}+\dfrac{2b}{y}+\dfrac{2c}{z}\)
2A=\(\dfrac{z+y}{x}+\dfrac{x+z}{y}+\dfrac{x+y}{z}\)
2A=\(\dfrac{z}{x}+\dfrac{y}{x}+\dfrac{x}{y}+\dfrac{z}{y}+\dfrac{x}{z}+\dfrac{y}{z}\)
2A=\(\left(\dfrac{z}{x}+\dfrac{x}{z}\right)+\left(\dfrac{y}{x}+\dfrac{x}{y}\right)+\left(\dfrac{z}{y}+\dfrac{y}{z}\right)\ge2+2+2=6\)
=>2A= \(\dfrac{2a}{x}+\dfrac{2b}{y}+\dfrac{2c}{z}\ge6\)
<=>A≥3 (chia cả 2 vế cho 2 ) (đpcm)
Xin góp thêm cách nữa:
Am-Gm thẳng cho 3 số:
\(\dfrac{a}{b+c-a}+\dfrac{b}{c+a-b}+\dfrac{c}{a+b-c}\ge3\sqrt[3]{\dfrac{abc}{\left(a+b-c\right)\left(b+c-a\right)\left(c+a-b\right)}}\)
việc còn lại chỉ việc chứng minh :
\(abc\ge\left(a+b-c\right)\left(b+c-a\right)\left(c+a-b\right)\)
Áp dụng BĐT Am-Gm ta có:
\(\left(a+b-c\right)\left(b+c-a\right)\le\dfrac{1}{4}\left(a+b-c+b+c-a\right)=b^2\)
\(\left(b+c-a\right)\left(c+a-b\right)\le c^2\)
\(\left(c+a-b\right)\left(a+b-c\right)\le a^2\)
Nhân lại ta có đpcm.Dấu = xảy ra khi a=b=c

C1 : Áp dụng bất đẳng thức AM - GM ta có :
\(\sum\dfrac{a}{b+c-a}\ge3\sqrt[3]{\dfrac{abc}{\left(a+b-c\right)\left(b+c-a\right)\left(c+a-b\right)}}\ge3\)
Dấu = xảy ra khi và chỉ khi a = b = c.
C2 : Theo Cauchy Schwarz :
\(\sum \frac{a}{b+c-a}\geq \sum \frac{a^2}{ab+ac-a^2}\geq \frac{(a+b+c)^2}{2(ab+ca+bc)-a^2-b^2-c^2}\geq \frac{(a+b+c)^2}{\frac{2}{3}(a+b+c)^2-\frac{1}{3}(a+b+c)^2}=3\)
(đpcm).
Đặt b+c-a=x, c+a-b=y, a+b-c=z thì 2a =y+z, 2b +x+z, 2c +x+y. Ta có:
\(\dfrac{2a}{b+c-a}+\dfrac{2b}{a+c-b}+\dfrac{2c}{a+b-c}\)
= \(\dfrac{y+z}{x}+\dfrac{x+z}{y}+\dfrac{x+y}{z}\)
=\(\left(\dfrac{y}{x}+\dfrac{x}{y}\right)+\left(\dfrac{z}{x}+\dfrac{x}{z}\right)+\left(\dfrac{z}{y}+\dfrac{y}{z}\right)\)(1)
Mà \(\dfrac{x}{y}+\dfrac{y}{x}-2=\dfrac{x^2+y^2-2xy}{xy}=\dfrac{\left(x-y\right)^2}{xy}\ge0\)( vì xy >0)
\(\Rightarrow\)\(\dfrac{x}{y}+\dfrac{y}{x}\ge2\)(2)
Tương tự: \(\dfrac{z}{x}+\dfrac{x}{z}\ge2\)(3)
\(\dfrac{z}{y}+\dfrac{y}{z}\ge2\)(4)
Từ (1),(2),(3) và (4):
\(\Rightarrow\)\(\left(\dfrac{y}{x}+\dfrac{x}{y}\right)+\left(\dfrac{z}{x}+\dfrac{x}{z}\right)+\left(\dfrac{z}{y}+\dfrac{y}{z}\right)\)\(\ge6\)
Hay \(\dfrac{2a}{b+c-a}+\dfrac{2b}{a+c-b}+\dfrac{2c}{a+b-c}\) \(\ge6\)
Do đó: \(\dfrac{a}{b+c-a}+\dfrac{b}{a+c-b}+\dfrac{c}{a+b-c}\ge3\)(đpcm)
Đặt: \(b+c-a=x\)
\(a+c-b=y\)
\(a+b-c=z\)
Suy ra:
\(2a=y+z\)
\(2b=x+z\)
\(2c=x+y\)
Ta có:
\(\dfrac{2a}{b+c-a}+\dfrac{2b}{a+c-b}+\dfrac{2c}{a+b-c}=\dfrac{y+z}{x}+\dfrac{x+z}{y}+\dfrac{x+y}{z}\)
\(=\left(\dfrac{y}{x}+\dfrac{x}{y}\right)+\left(\dfrac{z}{x}+\dfrac{x}{z}\right)+\left(\dfrac{z}{y}+\dfrac{y}{z}\right)\ge6\) ( BĐT luôn đúng)
=> ĐPCM
a,b,c là độ dài 3 cạnh t/g
\(\Rightarrow\dfrac{a}{b+c-a};\dfrac{b}{a+c-b};\dfrac{c}{a+b-c}>0\)
\(A=\dfrac{a}{b+c-a}+\dfrac{b}{a+c-b}+\dfrac{c}{a+b-c}\)
\(A+\dfrac{3}{2}=\dfrac{a}{b+c-a}+\dfrac{1}{2}+\dfrac{b}{a+c-b}+\dfrac{1}{2}+\dfrac{c}{b+a-c}+\dfrac{1}{2}\)
\(A+\dfrac{3}{2}=\dfrac{a+b+c}{2\left(b+c-a\right)}+\dfrac{a+b+c}{2\left(a+c-b\right)}+\dfrac{a+b+c}{2\left(b+a-c\right)}\)
\(A+\dfrac{3}{2}=\dfrac{\left(a+b+c\right)}{2}\left(\dfrac{1}{b+c-a}+\dfrac{1}{a+c-b}+\dfrac{1}{b+a-c}\right)\)
\(A+\dfrac{3}{2}\ge\dfrac{a+b+c}{2}\cdot\dfrac{9}{b+c-a+a+c-b+b+a-c}\)
\(A+\dfrac{3}{2}\ge\dfrac{9}{2}\)
\(\Rightarrow A\ge3\left(đpcm\right)\)