Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cách 1: Tính giá trị từng biểu thức trong ngoặc
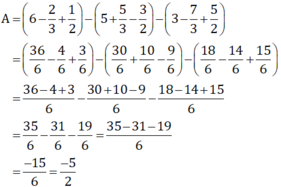
Cách 2: Bỏ dấu ngoặc rồi nhóm các số thích hợp
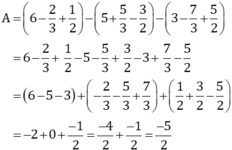

a) Ta có A = 21 + 22 + 23 + ... + 22022
2A = 22 + 23 + 24 + ... + 22023
2A - A = ( 22 + 23 + 24 + ... + 22023 ) - ( 21 + 22 + 23 + ... + 22022 )
A = 22023 - 2
Lại có B = 5 + 52 + 53 + ... + 52022
5B = 52 + 53 + 54 + ... + 52023
5B - B = ( 52 + 53 + 54 + ... + 52023 ) - ( 5 + 52 + 53 + ... + 52022 )
4B = 52023 - 5
B = \(\dfrac{5^{2023}-5}{4}\)
b) Ta có : A + 2 = 2x
⇒ 22023 - 2 + 2 = 2x
⇒ 22023 = 2x
Vậy x = 2023
Lại có : 4B + 5 = 5x
⇒ 4 . \(\dfrac{5^{2023}-5}{4}\) + 5 = 5x
⇒ 52023 - 5 + 5 = 5x
⇒ 52023 = 5x
Vậy x = 2023

Ta có : \(A=\frac{1}{1.2}+\frac{1}{3.4}+...+\frac{1}{99.100}\)
\(=1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+...+\frac{1}{99}-\frac{1}{100}\)
\(=\left(1+\frac{1}{3}+...+\frac{1}{99}\right)-\left(\frac{1}{2}+\frac{1}{4}+...+\frac{1}{100}\right)\)
\(=\left(1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+...+\frac{1}{99}+\frac{1}{100}\right)-2\left(\frac{1}{2}+\frac{1}{4}+...+\frac{1}{100}\right)\)
\(=\left(1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+...+\frac{1}{99}+\frac{1}{100}\right)-\left(1+\frac{1}{2}+...+\frac{1}{50}\right)\)
\(=\frac{1}{51}+\frac{1}{52}+...+\frac{1}{100}\)
\(B=\frac{2015}{51}+\frac{2015}{52}+...+\frac{2015}{100}\)
\(=2015\left(\frac{1}{51}+\frac{1}{52}+...+\frac{1}{100}\right)\)
\(\Rightarrow\) \(\frac{B}{A}=\frac{2015\left(\frac{1}{51}+\frac{1}{52}+...+\frac{1}{100}\right)}{\frac{1}{51}+\frac{1}{52}+...+\frac{1}{100}}=2015\)
\(\Rightarrow\) \(B⋮A\)
Ta có: A= 2 + 22 + 23 +.....+ 2100
Vì A là tổng các lũa thừa của 2 nên A chia hết cho 2
Ta có: A = 2 + 22 + 23 +.....+ 2100
=> A = (2 + 22) + (23 + 24) + ..... + (299 + 2100)
=> A = 1.(2 + 4) + 2.(2 + 4) + ...... + 298.(2 + 4)
=> A = 1.6 + 2.6 + ..... + 298.6
=> A = 6.(1 + 2 + .... + 298) chia hết cho 6
Ta có: A = 2 + 22 + 23 +.....+ 2100
=> A = (2 + 22 + 23 + 24) + ..... + (297 + 298 + 299 + 2100)
=> A = 1.(2 + 4 + 8 + 16) + .... + 296.(2 + 4 + 8 + 16)
=> A = 1.30 + .... + 296.30
=> A = 30.(1 + ..... + 296) chia hết cho 30