Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(CT:\overline{M}_2CO_3\)
\(n_{CO_2}=\dfrac{2.24}{22.4}=0.1\left(mol\right)\)
\(\overline{M}_2CO_3+2HCl\rightarrow2MCl+CO_2+H_2O\)
\(0.1.........................................0.1\)
\(M_{\overline{M}_2CO_3}=\dfrac{8.9}{0.1}=89\left(\dfrac{g}{mol}\right)\)
\(\Leftrightarrow2\overline{M}+60=89\)
\(\Leftrightarrow\overline{M}=14.5\)
Vì : thuộc hai chu kì liên tiếp nên hai kim loại là : \(Li,Na\)

Ap dụng tăng giảm khối lượng
\(n_{MCO_3}=\frac{20,6-18,4}{35,5.2-60}=0,2\)
\(M+60=18,4:0,2=92\Leftrightarrow M=32\)suy ra 2 nguyên tố đó là Mg và Ca

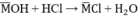
Theo pt: nHCl = nMOH = 0,1 (mol)
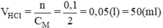
m(MCl) = 0,1.(31 + 35,5) = 6,65(g)

Gọi công thức muối cacbonat trung hòa của 2 kim loại kiềm cần tìm là R2CO3
\(R_2CO_3+2HCl\rightarrow2RCl+H_2O+CO_2\)
\(n_{CO_2}=n_{R_2CO_3}=\dfrac{2,24}{22,4}=0,1\left(mol\right)\\ \Rightarrow M_{R_2CO_3}=2M_R+60=\dfrac{9,1}{0,1}=91\\ \Rightarrow M_R=15,5\)
Do 2 kim loại kiềm ở chu kì liên tiếp nhau
=> 2 kim loại đó là Li, Na

Gọi nguyên tử khối trung bình của 2 kim loại kiềm thuộc 2 chu kì liên tiếp đó là R
\(BTNT\left(R\right):n_R=n_{RCl}\\ \Rightarrow\dfrac{5,4}{R}=\dfrac{15,95}{R+35,5}\\ \Rightarrow R=18,17\)
=> 2 kim loại cần tìm là Li và Na

Đặt tên chung của 2 kim loại A,B đó là Z \(\left(M_A< M_Z< M_B\right)\)
\(2M+2HCl\rightarrow2MCl+H_2\\ n_{HCl}=n_M=n_{Cl^-}=\dfrac{18,65-8}{35,5}=0,3\left(mol\right)\\ \Rightarrow M_Z=\dfrac{8}{0,3}\approx26,667\left(\dfrac{g}{mol}\right)\\ \Rightarrow\left\{{}\begin{matrix}A:Natri\left(Na=23\right)\\B:Kali\left(K=39\right)\end{matrix}\right.\)



\(CT:\overline{M}_2CO_3\)
\(n_{CO_2}=\dfrac{2.24}{22.4}=0.1\left(mol\right)\)
\(\overline{M}_2CO_3+2HCl\rightarrow2\overline{M}Cl+CO_2+H_2O\)
\(.............0.2..............0.1.....0.1\)
\(m_{HCl}=0.2\cdot36.5=7.3\left(g\right)\)
\(m_{CO_2}=0.1\cdot44=4.4\left(g\right)\)
\(m_{H_2O}=0.1\cdot18=1.8\left(g\right)\)
\(BTKL:m_{hh}+m_{HCl}=m_{Muối}+m_{CO_2}+m_{H_2O}\)
\(\Leftrightarrow8.9+7.3=m_{Muối}+4.4+1.8\)
\(\Leftrightarrow m_{muối}=8.9+7.3-4.4-1.8=10\left(g\right)\)