Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có :
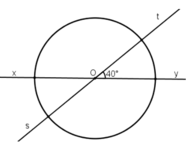
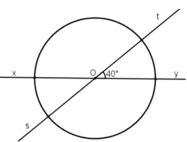
\(\widehat{xOs}\)= 400(theo giải thiết)
\(\widehat{tOy}\)=400( đối đỉnh với \(\widehat{xOs}\))
\(\widehat{xOt}\) + \(\widehat{tOy}\)= 1800
\(\Rightarrow\widehat{xOt}\) = \(\widehat{tOy}\) \(=180^0-40^0=140^0\)
\(\widehat{yOs}=140^0\)(đối đỉnh với \(\widehat{xOt}\))
\(\widehat{xOy}=\widehat{sOt}=180^0\)

Bài này hôm qua mình giải rồi. bạn xem bài những bài giải lớp 9 ngày hôm qua sẽ có nhé

Trên mặt phẳng cho n > = điểm sao cho khoảng cách giữa 2 điểm bất kì đôi một khác nhau. Người ta nối mỗi điểm với điểm gần nhất.
CMR qua mỗi điểm co không quá 5 đoạn thẳng

Bài 1:
Đặt: (d): y = (m+5)x + 2m - 10
Để y là hàm số bậc nhất thì: m + 5 # 0 <=> m # -5
Để y là hàm số đồng biến thì: m + 5 > 0 <=> m > -5
(d) đi qua A(2,3) nên ta có:
3 = (m+5).2 + 2m - 10
<=> 2m + 10 + 2m - 10 = 3
<=> 4m = 3
<=> m = 3/4
(d) cắt trục tung tại điểm có tung độ bằng 9 nên ta có:
9 = (m+5).0 + 2m - 10
<=> 2m - 10 = 9
<=> 2m = 19
<=> m = 19/2
(d) đi qua điểm 10 trên trục hoành nên ta có:
0 = (m+5).10 + 2m - 10
<=> 10m + 50 + 2m - 10 = 0
<=> 12m = -40
<=> m = -10/3
(d) // y = 2x - 1 nên ta có:
\(\hept{\begin{cases}m+5=2\\2m-10\ne-1\end{cases}}\) <=> \(\hept{\begin{cases}m=-3\\m\ne\frac{9}{2}\end{cases}}\) <=> \(m=-3\)
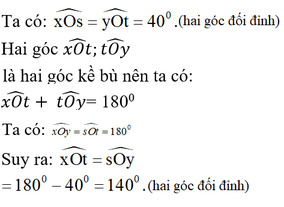
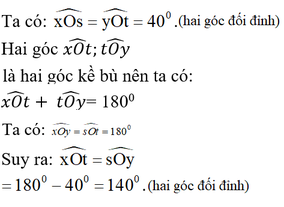

Ta chọn điểm O bất kì nằm trong mặt phẳng chứa 5 đường thẳng ấy. Qua O ta dựng các đường thẳng song song với các đường thẳng đã cho , khi đó có 10 góc đôi một đối đỉnh qua O . Vậy sẽ có ít nhất một góc không vượt quá \(\frac{180^o}{5}=36^o\)
'
'
'
'
'
'