Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Gọi công bội của cấp số nhân là q => b=a.q; c=a.q^2
Gọi công sai của cấp số cộng là d => b=a+2d; c=a+8d
Ta có: a.q=a+2d => \(q=\dfrac{a+2d}{a}=1+2\dfrac{d}{a}\)
\(a.q^2=a+8d\Rightarrow q^2=\dfrac{a+8d}{a}=1+8\dfrac{d}{a}\)
Suy ra \(\left(1+2\dfrac{d}{a}\right)^2=1+8\dfrac{d}{a}\Rightarrow\dfrac{d}{a}=1\left(d\ne0\right)\)
=> b=a+2a=3a; c=a+8a=9a
Theo bài ra a+b+c=26 => a+3a+9a=13a=26 => a=2; b=6; c=18
Vậy ba số cần tìm là a=2; b=6; c=18
+ Gọi số hạng đầu của cấp số nhân là u1, công bội là x
Theo giả thiết ta có hệ phương trình
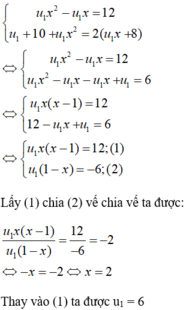
+ Tổng của năm số hạng đầu của CSN là:
Gọi 3 số hạng của cấp số cộng là: \(5;5+d;5+2d\)
Gọi 3 số hạng của cấp số nhân là: \(5;5q;5q^2\).
Ta có hệ sau:\(\left\{{}\begin{matrix}5+2d=5q^2\\5+d=5q+10\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}5+2d=5q^2\\d=5q+5\end{matrix}\right.\)\(\Rightarrow5+2.\left(5q+5\right)=5q^2\)\(\Rightarrow\left\{{}\begin{matrix}q=-1\\q=3\end{matrix}\right.\).
Với \(q=-1\) thì \(d=5.q+5=5.\left(-1\right)+5=0\).
Với \(q=3\) thì \(d=5.q+5=5.3+5=20\).
Vậy
Với \(q=-1\):
3 số hạng của cấp số cộng là: 5; 5; 5.
3 số hạng của cấp số nhân là: 5; - 5; 5.
Với \(q=3\):
3 số hạng của cấp số cộng là: 5; 25; 45.
3 số hạng của cấp số nhân là: 5; 15; 45.
Gọi ba số đã cho u1,u2,u7 theo thứ tự là ba số của một cấp số cộng (un) và v1,v2, v3 của cấp số nhân (vn) . Theo giả thiết Ta có hệ:
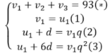
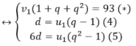
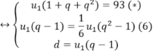
Giải phương trình (6)
( 6 ) ⇔ u 1 q − 1 = 1 6 u 1 q − 1 q + 1 ⇔ u 1 q − 1 = 0 ( l o a i ) 1 = 1 6 q + 1
Thay vào (*), ta được
u 1 1 + 5 + 5 2 = 93 ⇔ u 1 = 3 = v 1
Suy ra
u 2 = u 1 . q = 3.5 = 15 = v 2 u 3 = u 1 . q 2 = 3.25 = 75 = v 3
Vậy tích ba số v 1 . v 2 . v 3 = 3.15.75 = 3375
Đáp án A
Gọi 3 số đã cho là \(u_1;u_2;u_3\), theo thứ tự là 3 số của một cấp số cộng
Còn cấp số nhân \(\left(v_n\right)\). Theo giả thiết ta có hệ :
\(\Leftrightarrow\begin{cases}v_1+v_2+v_3+v_4=93\left(a\right)\\v_1=u\left(1\right)_1\\u_1+d=v_1q\left(2\right)\\u_1+2d=v_1q^2\left(3\right)\end{cases}\)
\(\Leftrightarrow\begin{cases}v_1\left(1+q+q^2\right)=93\left(a\right)\\d=u_1\left(q-1\right)\left(1V2\right)\left(4\right)\\6d=u_3-u_1=u_1\left(q^2-1\right)\left(2V3\right)\left(5\right)\end{cases}\)
\(\Leftrightarrow\begin{cases}u_1\left(1+q+q^2\right)=93\left(a\right)\\u_1\left(q-1\right)=\frac{1}{6}u_1\left(q^2-1\right)\left(4V5\right)\left(6\right)\\d=u_1\left(q-1\right)\end{cases}\)
Từ (1) và (2) cho ta phương trình (4). Còn từ (2) và (3) cho phương trình (5). Mặt khác ừ (4) và (5) cho phương trình (6)
Do \(u_1\ne0,q\ne1\Rightarrow\left(6\right)\Leftrightarrow1=\frac{1}{6}\left(q+1\right)\Leftrightarrow q=5\)
Theo (a) : \(v_1+5v_1+25v_1=93\Leftrightarrow u_1=3\)
Vậy 3 số cần tìm là : 3,15,75
Chọn C.
Gọi u1; u2; u3 theo thứ tự đó lập thành một cấp số nhân.
Theo đề: u1 – 1; u2; u3 – 19 theo thứ tự đó lập thành một cấp số cộng.
Ta có: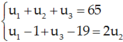
Lấy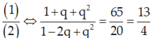
⇔ 4(1 + q + q2) = 13(1 – 2q + q2)
⇔ 9q2 – 30q + 9 = 0 ⇔ q = 3 ∨ q = 1/3
Vì u1; u2; u3 theo thứ tự lập thành cấp số nhân tăng dần nên chọn q = 3 khi đó u1 = 5
Do đó u1 = 5; u2 = 15; u3 = 45
Vậy số lớn nhất trong 3 số là 45.