Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án B
Từ giả thiết ta có
b 2 = a c a + c = 2 ( b + 8 ) b + 8 2 = a ( c + 64 ) ⇔ b 2 = a c a + c = 2 ( b + 8 ) b + 8 2 = b 2 + 64 a ⇔ b 2 = a c c = 7 a + 8 b = 4 a − 4
⇔ 4 a - 4 2 = a 7 a + 8 c = 7 a + 8 b = 4 a - 4 ⇔ 9 a 2 - 40 a + 16 = 0 c = 7 a + 8 b = 4 a - 4 ⇔ a = 4 ; b = 12 ; c = 36 a = 4 9 ; b = - 20 9 ; c = 100 9
Do a,b,c tạo thành một dãy số tăng nên a = 4 ; b = 12 ; c = 36 .
Suy ra
a − b + 2 c = 4 − 12 + 2.36 = 64.
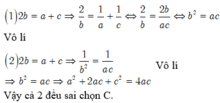
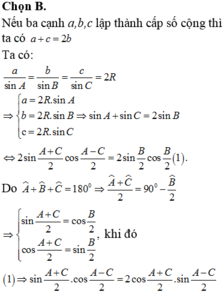
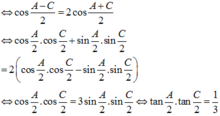
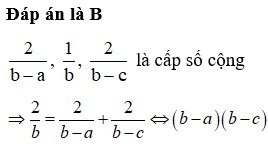
Chọn C.
Phương pháp: Sử dụng định nghĩa về cấp số cộng.
Cách giải: Vì a, b, c theo thứ tự lập thành một cấp số cộng nên