Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

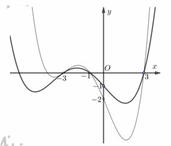
Đáp án A.
Phương trình hoành độ giao điểm của đồ thị (C) với đường thẳng đã cho là
x − 1 1 − 2 x = x + m ⇔ x − 1 = 1 − 2 x x + m
(do x = 1 2 không là nghiệm)
⇔ 2 x 2 + 2 m x − m − 1 = 0 (*).
Đồ thị (C) với đường thẳng đã cho cắt nhau tại hai điểm phân biệt khi và chỉ khi (*) có hai nghiệm phân biệt ⇔ m 2 + 2 m + 2 > 0 (nghiệm đúng với mọi m).
Giả sử E x 1 ; y 1 , F x 2 ; y 2 thì x 1 , x 2 là hai nghiệm của (*).
Suy ra x 1 + x 2 = − m ; x 1 x 2 = − m + 1 2 .
Do đó 2 x 1 − 1 2 x 2 − 1 = 4 x 1 x 2 − 2 x 1 + x 2 + 1 = − 1 .
Ta có
k 1 = − 1 2 x 1 − 2 2 ; k 2 = − 1 2 x 2 − 1 2
nên k 1 k 2 = 1 .
Suy ra S ≥ 2 k 1 2 k 2 2 − 3 k 1 k 2 = − 1 . Dấu bằng xảy ra khi k 1 = − 1 k 2 = − 1 ⇒ x 1 = 0 x 2 = 1 hoặc x 1 = 1 x 2 = 0 ⇒ m = − 1 . Vậy S đạt giá trị nhỏ nhất bằng ‒1.


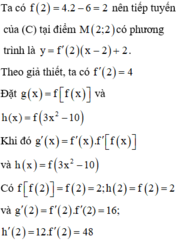






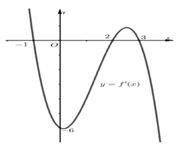
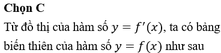
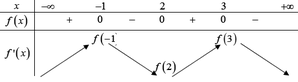

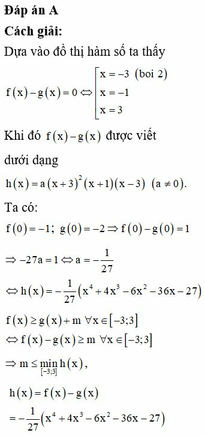
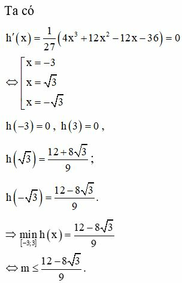


Chọn B