Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tham khảo:
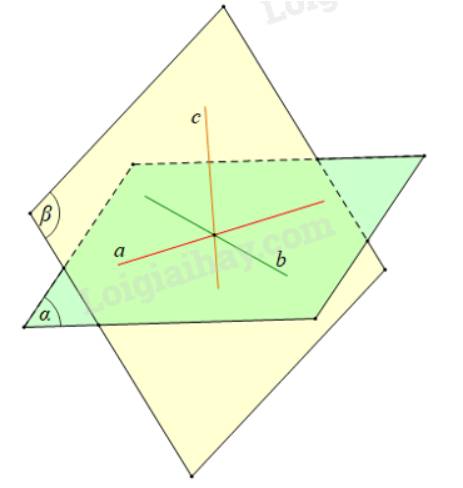
Giả sử a ∩ b = {I} và α = mp(a, b);
a ∩ c = {J} và β = mp(a, c);
b ∩ c = {K} và γ = mp(b, c) với các điểm I, J, K phân biệt.
Khi đó α ∩ β = a và đường thẳng a chính là đường thẳng IJ.
α ∩ γ = b và đường thẳng b chính là đường thẳng IK.
β ∩ γ = c và đường thẳng c chính là đường thẳng JK.
Mà chỉ có một mặt phẳng duy nhất đi qua ba điểm I, J, K, đó là (IJK)
Khi đó a, b, c cùng thuộc mặt phẳng (IJK), điều này trái với giả thiết a, b, c không cùng nằm trong một mặt phẳng.
Vậy I, J, K phải trùng nhau hay a, b, c đồng quy.

Gọi I = d1 ∩ d2; (P) là mặt phẳng chứa (d1) và (d2).
Gọi d3 ∩ d1 = M; d3 ∩ d2 = N.
+ M ∈ d1, mà d1 ⊂ (P) ⇒ M ∈ (P)
+ N ∈ d2, mà d2 ⊂ (P) ⇒ N ∈ (P).
Nếu M ≠ N ⇒ d3 có hai điểm M, N cùng thuộc (P)
⇒ d3 ⊂ (P)
⇒ d1; d2; d3 đồng phẳng (trái với giả thiết).
⇒ M ≡ N
⇒ M ≡ N ≡ I
Vậy d1; d2; d3 đồng quy.