K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
VQ
30 tháng 3 2019
Vì 0<a,b<\(\frac{\pi}{2}\)nên tana,tanb>0 ⇒ tana+tanb>0
ta có tan(a+b)=\(\frac{tana+tanb}{1-tana.tanb}\) ⇔tana+tanb=tan(a+b)(1-3+2\(\sqrt{2}\))
⇔tana+tanb=tan(\(\frac{\pi}{4}\)).(-2+2\(\sqrt{2}\))=-2+2\(\sqrt{2}\)(thỏa)
ta có \(\left\{{}\begin{matrix}tana.tanb=3-2\sqrt{2}\\tana+tanb=-2+2\sqrt{2}\end{matrix}\right.\)
áp đụng hệ thức Vi-et đảo ta có: tana và tanb là hai nghiệm của phương trình: X2+(2-2\(\sqrt{2}\))X+3-2\(\sqrt{2}\)=0
bấm máy giải phương trình trên ta được 2 nghiệm x1,x2
Vậy (tana;tanb)=(x1;x2) hoặc (x2;x1) và tana.tanb=3-2\(\sqrt{2}\)
AH
Akai Haruma
Giáo viên
11 tháng 4 2018
Câu a)
Ta sử dụng 2 công thức:
\(\bullet \tan (180-\alpha)=-\tan \alpha\)
\(\bullet \tan (\alpha+\beta)=\frac{\tan \alpha+\tan \beta}{1-\tan \alpha.\tan \beta}\)
Áp dụng vào bài toán:
\(\text{VT}=\tan A+\tan B+\tan C=\tan A+\tan B+\tan (180-A-B)\)
\(=\tan A+\tan B-\tan (A+B)=\tan A+\tan B-\frac{\tan A+\tan B}{1-\tan A.\tan B}\)
\(=(\tan A+\tan B)\left(1+\frac{1}{1-\tan A.\tan B}\right)=(\tan A+\tan B).\frac{-\tan A.\tan B}{1-\tan A.\tan B}\)
\(=-\tan A.\tan B.\frac{\tan A+\tan B}{1-\tan A.\tan B}=-\tan A.\tan B.\tan (A+B)\)
\(=\tan A.\tan B.\tan (180-A-B)\)
\(=\tan A.\tan B.\tan C=\text{VP}\)
Do đó ta có đpcm
Tam giác $ABC$ có ba góc nhọn nên \(\tan A, \tan B, \tan C>0\)
Áp dụng BĐT Cauchy ta có:
\(P=\tan A+\tan B+\tan C\geq 3\sqrt[3]{\tan A.\tan B.\tan C}\)
\(\Leftrightarrow P=\tan A+\tan B+\tan C\geq 3\sqrt[3]{\tan A+\tan B+\tan C}\)
\(\Rightarrow P\geq 3\sqrt[3]{P}\)
\(\Rightarrow P^3\geq 27P\Leftrightarrow P(P^2-27)\geq 0\)
\(\Rightarrow P^2-27\geq 0\Rightarrow P\geq 3\sqrt{3}\)
Vậy \(P_{\min}=3\sqrt{3}\). Dấu bằng xảy ra khi \(\angle A=\angle B=\angle C=60^0\)
AH
Akai Haruma
Giáo viên
11 tháng 4 2018
Câu b)
Ta sử dụng 2 công thức chính:
\(\bullet \tan (\alpha+\beta)=\frac{\tan \alpha+\tan \beta}{1-\tan \alpha.\tan \beta}\)
\(\bullet \tan (90-\alpha)=\frac{1}{\tan \alpha}\)
Áp dụng vào bài toán:
\(\text{VT}=\tan \frac{A}{2}.\tan \frac{B}{2}+\tan \frac{B}{2}.\tan \frac{C}{2}+\tan \frac{C}{2}.\tan \frac{A}{2}\)
\(=\tan \frac{A}{2}.\tan \frac{B}{2}+\tan \frac{C}{2}(\tan \frac{A}{2}+\tan \frac{B}{2})\)
\(=\tan \frac{A}{2}.\tan \frac{B}{2}+\tan (90-\frac{A+B}{2})(\tan \frac{A}{2}+\tan \frac{B}{2})\)
\(=\tan \frac{A}{2}.\tan \frac{B}{2}+\frac{\tan \frac{A}{2}+\tan \frac{B}{2}}{\tan (\frac{A+B}{2})}\)
\(=\tan \frac{A}{2}.\tan \frac{B}{2}+\frac{\tan \frac{A}{2}+\tan \frac{B}{2}}{\frac{\tan \frac{A}{2}+\tan \frac{B}{2}}{1-\tan \frac{A}{2}.\tan \frac{B}{2}}}\)
\(=\tan \frac{A}{2}.\tan \frac{B}{2}+1-\tan \frac{A}{2}.\tan \frac{B}{2}=1=\text{VP}\)
Ta có đpcm.
Cũng giống phần a, ta biết do ABC là tam giác nhọn nên
\(\tan A, \tan B, \tan C>0\)
Đặt \(\tan A=x, \tan B=y, \tan C=z\). Ta có: \(xy+yz+xz=1\)
Và \(T=x+y+z\)
\(\Rightarrow T^2=x^2+y^2+z^2+2(xy+yz+xz)\)
Theo hệ quả quen thuộc của BĐT Cauchy:
\(x^2+y^2+z^2\geq xy+yz+xz\)
\(\Rightarrow T^2\geq 3(xy+yz+xz)=3\)
\(\Rightarrow T\geq \sqrt{3}\Leftrightarrow T_{\min}=\sqrt{3}\)
Dấu bằng xảy ra khi \(x=y=z=\frac{1}{\sqrt{3}}\Leftrightarrow \angle A=\angle B=\angle C=60^0\)
PD
0
LA
1
NV
Nguyễn Việt Lâm
Giáo viên
24 tháng 4 2021
\(1=tan\left(\dfrac{\pi}{4}\right)=tan\left(a+b\right)=\dfrac{tana+tanb}{1-tana.tanb}\)
\(\Rightarrow tana+tanb=1-tana.tanb\)
\(\Rightarrow tana+tanb+tana.tanb=1\)
Do đó:
\(M=1+tana+tanb+tana.tanb=1+1=2\)
TC
1
AH
Akai Haruma
Giáo viên
25 tháng 4 2018
Lời giải:
Sử dụng các công thức sau:
\(\bullet \tan \alpha=\frac{1}{\cot \alpha}\)
\(\bullet \tan (\alpha+\beta)=\frac{\tan \alpha+\tan \beta}{1-\tan\alpha.\tan \beta}\)
Ta có:
\(\text{VT}=\frac{1}{\tan a+\tan b}-\frac{1}{\cot a+\cot b}=\frac{1}{\tan a+\tan b}-\frac{1}{\frac{1}{\tan a}+\frac{1}{\tan b}}\)
\(=\frac{1}{\tan a+\tan b}-\frac{\tan a\tan b}{\tan a+\tan b}=\frac{1-\tan a\tan b}{\tan a+\tan b}\)
\(=\frac{1}{\frac{\tan a+\tan b}{1-\tan a\tan b}}=\frac{1}{\tan (a+b)}=\cot (a+b)=\text{VP}\)
Ta có đpcm.
PT
1
CM
6 tháng 5 2018
Chọn B.
Theo công thức cộng ta có:
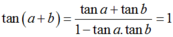
Mà a và b là các góc nhọn suy ra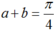 
TN
1
HN
13 tháng 2 2017
Ta có: \(a^2=b^2+c^2-2bc\cos A\)
\(\Leftrightarrow\cos A=\frac{b^2+c^2-a^2}{2bc}\)
Tương tự: \(\Leftrightarrow\cos B=\frac{a^2+c^2-b^2}{2ac}\)
Ta lại có: \(\frac{a}{\sin A}=\frac{b}{\sin B}=2R\)
\(\left\{\begin{matrix}\sin A=\frac{a}{2R}\\\sin B=\frac{b}{2R}\end{matrix}\right.\)
Quay lại bài toán ta có:
\(\frac{\tan A}{\tan B}=\frac{\sin A\cos B}{\sin B\cos A}=\frac{\frac{a}{2R}.\frac{a^2+c^2-b^2}{2ac}}{\frac{b}{2R}.\frac{b^2+c^2-a^2}{2bc}}=\frac{c^2+a^2-b^2}{c^2+b^2-a^2}\)
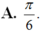
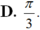
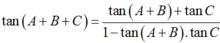
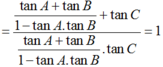
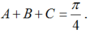
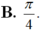
\(tan\left(a+b\right)=\dfrac{tana+tanb}{1-tana.tanb}=1\)
\(\Rightarrow a+b=45^0\)
chỉ e cách tính ik, cái này tắt quá ;-;