Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì \(\widehat A = \widehat E\), \(\widehat C = \widehat D\) nên đỉnh A tương ứng với đỉnh E, đỉnh C tương ứng với đỉnh D.
\( \Rightarrow \widehat B = \widehat F\) ( 2 góc tương ứng)
Do đó, \(\Delta{ABC}=\Delta{EFD}\)
\(\Rightarrow AB = DE;BC = EF;AC = DF\)( các cạnh tương ứng )

a) Các tia Om, On tương ứng là tia phân giác của góc yOz và xOz vì:
Tia Om nằm trong góc yOz và \(\widehat {yOm} = \widehat {mOz}\)
Tia On nằm trong góc xOz và \(\widehat {xOn} = \widehat {nOz}\)
b) Vì các tia Om, On tương ứng là tia phân giác của góc yOz và xOz nên: \(\widehat {yOm} = \widehat {mOz} = \frac{1}{2}.\widehat {yOz};\widehat {xOn} = \widehat {nOz} = \frac{1}{2}.\widehat {xOz}\)
Mà tia Oz nằm trong góc xOy nên \(\widehat {yOz} + \widehat {xOz} = \widehat {xOy}\)
\( \Rightarrow \widehat {mOz} + \widehat {zOn} = \frac{1}{2}.\widehat {yOz} + \frac{1}{2}.\widehat {xOz} = \frac{1}{2}.\widehat {xOy}\)
Mà tia Oz nằm trong góc mOn nên \(\widehat {mOz} + \widehat {zOn} = \widehat {mOn}\) và \(\widehat {xOy} = 90^\circ \)
\( \Rightarrow \widehat {mOn} = \frac{1}{2}.90^\circ = 45^\circ \)

Theo đề ra ta có :
\(\Rightarrow\hept{\begin{cases}A-B=40^o\\A+B=90^o\end{cases}}\)
Góc A sẽ bằng:
(90 + 40) :2 = 65o
Góc B sẽ bằng :
90o - 65o = 25o
Vậy ...............
Theo de bai ta co :
A-B=40°
A+B=90°
Goc A se bang :
(90+40):2=65°
Goc B se bang :
90°-65°=25°
Dap so : ......

Vì \(\widehat{A}-\widehat{B}=\widehat{B}-\widehat{C}\) nên \(\widehat{A}-2\widehat{B}+\widehat{C}=0\)
\(\Rightarrow\left\{{}\begin{matrix}\widehat{A}-2\widehat{B}+\widehat{C}=0^0\left(1\right)\\\widehat{A}+\widehat{B}+\widehat{C}=180^0\left(2\right)\end{matrix}\right.\)
Trừ \(\left(2\right)\) cho \(\left(1\right)\), ta được \(3\widehat{B}=180^0\Rightarrow\widehat{B}=60^0\)
\(\Rightarrow\widehat{A}+\widehat{C}=120^0\)
Vậy GTLN của \(\widehat{A}\) là \(119^0\) vì \(\widehat{C}>0\)

làm tương tự
Bài 1 Cho tam giác ABC có góc A= 40 độ,AB=AC.Gọi M Là trung điểm của BC tính các góc của mỗi tam giác AMB và tam giác AMC
bài làm
Bài 1:
-Vì M là trung điểm nên CM=BM
-Vì AM chung và theo GT AB=AC nên Tam giác ABM=tam giac ACM
Góc A=40 độ=>Góc MAB=MAC=20
Vì góc AMB+góc AMC=180 độ(2 góc kề bù) mà góc AMB=AMC nên AMB=AMC=90 độ(2 góc tương ứng)
=>góc ABM=góc ACM=70 độ
Vậy Góc A=Góc C=70 độ
Góc AMC=góc AMB=90 độ
Góc CAM=góc BAM=20 độ
Thanks nhá

\(1,\widehat{A}+\widehat{B}+\widehat{C}=180^0\\ \text{Mà }\widehat{A}=\widehat{B}=\widehat{C}\\ \Rightarrow\widehat{A}=\widehat{B}=\widehat{C}=\dfrac{180^0}{3}=60^0\\ 2,\widehat{A}+\widehat{B}+\widehat{C}=180^0\\ \Rightarrow\widehat{B}+\widehat{C}=180^0-\widehat{A}=110^0\\ \text{Mà }\widehat{B}-\widehat{C}=10^0\\ \Rightarrow\left\{{}\begin{matrix}\widehat{B}=\left(110^0+10^0\right):2=60^0\\\widehat{C}=60^0-10^0=50^0\end{matrix}\right.\)

a) Hai góc \(\widehat {xOy}\) và \(\widehat {yOz}\) có cạnh Oy chung, không có điểm trong chung
b) Ta có:
\(\begin{array}{l}\widehat {xOy} = 30^\circ ,\widehat {yOz} = 45^\circ ,\widehat {xOz} = 75^\circ \\ \Rightarrow \widehat {xOy} + \widehat {yOz} = \widehat {xOz}\end{array}\)
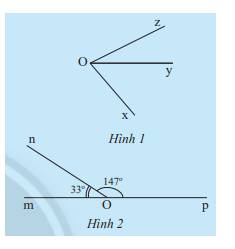
c) Ta có: \(\widehat {mOn} + \widehat {nOp} = 33^\circ + 147^\circ = 180^\circ \)