Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(MA.MB=MC.MD\Leftrightarrow\Delta MAC\approx\Delta MDB\left(G-G\right)\)
Duong thang OM cat duong tron tai E,F
chung minh tuong tu ta co \(MA.MB=ME.MF=\left(R-d\right)\left(R+d\right)=R^2-d^2\)

a.
Gọi D là trung điểm BC \(\Rightarrow OD\perp BC\)
Gọi E là trung điểm AM \(\Rightarrow OE\perp AM\)
\(\Rightarrow\) Tứ giác OEMD là hình chữ nhật (có 3 góc vuông)
\(\Rightarrow MD=OE\) và \(ME=OD\)
\(MA^2+MB^2+MC^2=MA^2+\left(BD-MD\right)^2+\left(DC+MD\right)^2\)
\(=\left(2ME\right)^2+\left(BD-MD\right)^2+\left(BD+MD\right)^2\) (do \(BD=CD\))
\(=4ME^2+2BD^2+2MD^2\)
\(=2\left(ME^2+BD^2\right)+2\left(ME^2+MD^2\right)\)
\(=2\left(OD^2+BD^2\right)+2\left(OD^2+MD^2\right)\)
\(=2OB^2+2OM^2\)
\(=2R^2+2r^2\) cố định (đpcm)
b. Gọi G là giao điểm OM và AD
Theo c/m câu a ta có \(\left\{{}\begin{matrix}OD||AM\\OD=EM=\dfrac{1}{2}AM\end{matrix}\right.\)
Theo định lý Talet: \(\dfrac{DG}{AG}=\dfrac{OD}{AM}=\dfrac{OG}{GM}=\dfrac{1}{2}\Rightarrow\left\{{}\begin{matrix}AG=\dfrac{2}{3}AD\\OG=\dfrac{1}{3}OM\end{matrix}\right.\)
Do O, M cố định \(\Rightarrow\) G cố định
Mặt khác trong tam giác ABC do D là trung điểm AB \(\Rightarrow\) AD là trung tuyến
Mà \(AG=\dfrac{2}{3}AD\Rightarrow\) G là trọng tâm tam giác ABC
\(\Rightarrow\) Trọng tâm tam giác ABC cố định

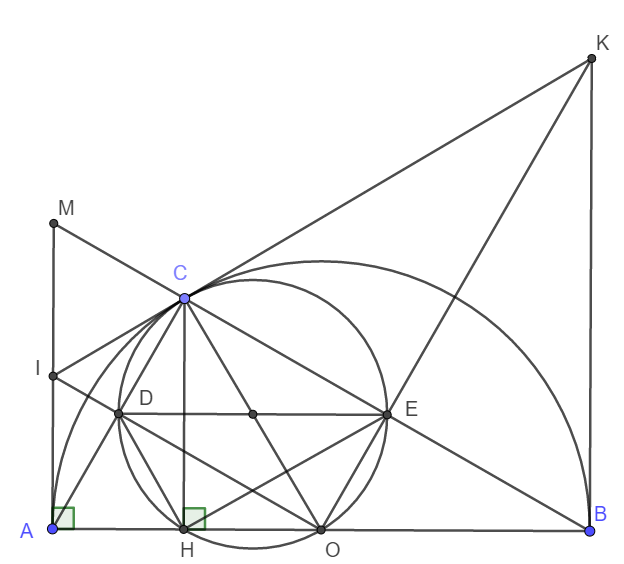
a) Do C thuộc nửa đường tròn nên \(\widehat{ACB}=90^o\) hay AC vuông góc MB.
Xét tam giác vuông AMB có đường cao AC nên áp dụng hệ thức lượng ta có:
\(BC.BM=AB^2=4R^2\)
b) Xét tam giác MAC vuông tại C có CI là trung tuyến ứng với cạnh huyền nên IM = IC = IA
Vậy thì \(\Delta ICO=\Delta IAO\left(c-c-c\right)\)
\(\Rightarrow\widehat{ICO}=\widehat{IAO}=90^o\)
Hay IC là tiếp tuyến tại C của nửa đường tròn.
c) Xét tam giác vuông AMB có đường cao AC, áp dụng hệ thức lượng ta có:
\(MB.MC=MA^2=4IC^2\Rightarrow IC^2=\frac{1}{4}MB.MC\)
Xét tam giác AMB có I là trung điểm AM, O là trung điểm AB nên IO là đường trung bình tam giác ABM.
Vậy thì \(MB=2OI\Rightarrow MB^2=4OI^2\) (1)
Xét tam giác vuông MAB, theo Pi-ta-go ta có:
\(MB^2=MA^2+AB^2=MA^2+4R^2\) (2)
Từ (1) và (2) suy ra \(4OI^2=MA^2+4R^2.\)
d) Do IA, IC là các tiếp tuyến cắt nhau nên ta có ngay \(AC\perp IO\Rightarrow\widehat{CDO}=90^o\)
Tương tự \(\widehat{CEO}=90^o\)
Xét tứ giác CDOE có \(\widehat{CEO}=\widehat{CDO}=90^o\)mà đỉnh E và D đối nhau nên tứ giác CDOE nội tiếp đường tròn đường kính CO.
Xét tứ giác CDHO có: \(\widehat{CHO}=\widehat{CDO}=90^o\) mà đỉnh H và D kề nhau nên CDHO nội tiếp đường tròn đường kính CO.
Vậy nên C, D, H , O, E cùng thuộc đường tròn đường kính CO.
Nói cách khác, O luôn thuộc đường tròn ngoại tiếp tam giác HDE.
Vậy đường tròn ngoại tiếp tam giác HDE luôn đi qua điểm O cố định.
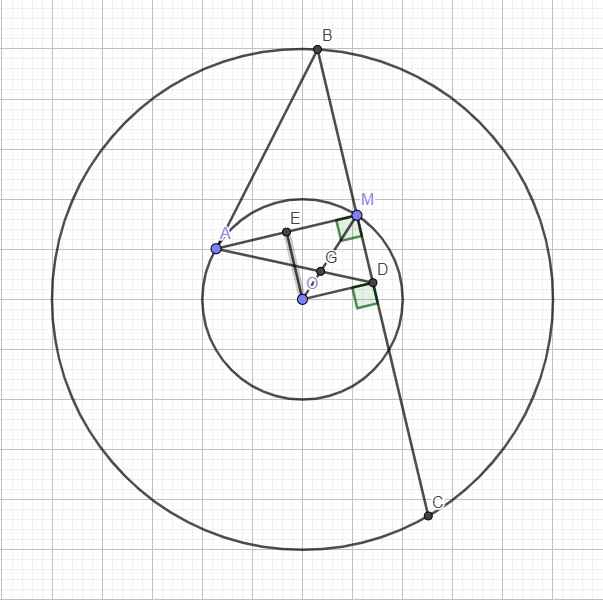
M A B C O N D
Gọi \(BC\) cắt \(\left(O;r\right)\) lần thứ hai tại \(N\), \(CD\) là đường kính của \(\left(O;R\right)\)
Do hình chiếu vuông góc của \(O\) trên \(BC\) là trung điểm của \(MN,BC\) nên \(MB=NC\)
Tính đối xứng tâm của đường tròn nên \(NC=AD,NC||AD\) hay \(MB=||AD\)
Suy ra \(AM=DB\). Ta biến đổi:
\(MA^2+MB^2+MC^2=MA^2+\left(MB+MC\right)^2-2MB.MC\)
\(=DB^2+BC^2-2\left(R^2-OM^2\right)=\left(2R\right)^2-2\left(R^2-r^2\right)=2\left(R^2+r^2\right)\)