Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Gọi d là đường thẳng qua M có véc tơ chỉ phương:
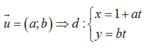
- Đường tròn (C1) tâm I1 (1;1) và R1= 1
Đường tròn (C2) : tâm I2( -2;0) và R2= 3
- Nếu d cắt (C1) tại A :
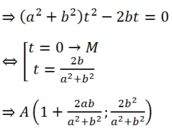
- Nếu d cắt (C2) tại B:
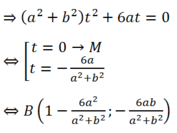
- Theo giả thiết: MA= 2 MB nên MA2= 4 MB2 (*)
- Ta có :
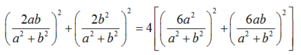
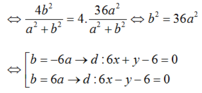

Đường tròn (C) tâm \(I\left(2;-1\right)\) bán kính \(R=2\sqrt{5}\)
Gọi H là trung điểm AB \(\Rightarrow IH\perp AB\Rightarrow IH=d\left(I;\Delta\right)\)
\(S_{IAB}=\dfrac{1}{2}IH.AB=\dfrac{1}{2}IH.2AH=IH.\sqrt{IA^2-IH^2}=IH.\sqrt{20-IH^2}\)
\(\Rightarrow IH\sqrt{20-IH^2}=8\)
\(\Rightarrow IH^4-20IH^2+64=0\Rightarrow\left[{}\begin{matrix}IH=4\\IH=2\end{matrix}\right.\)
\(\overrightarrow{IM}=\left(-1;-2\right)\Rightarrow IM=\sqrt{5}\), mà \(IH\le IM\Rightarrow IH=2\)
Gọi \(\left(a;b\right)\) là 1 vtpt của \(\Delta\) với a;b không đồng thời bằng 0
\(\Rightarrow\) Phương trình \(\Delta\): \(a\left(x-1\right)+b\left(y+3\right)=0\Leftrightarrow ax+by-a+3b=0\)
\(d\left(I;\Delta\right)=IH\Leftrightarrow\dfrac{\left|2a-b-a+3b\right|}{\sqrt{a^2+b^2}}=2\)
\(\Leftrightarrow\left|a+2b\right|=2\sqrt{a^2+b^2}\)
\(\Leftrightarrow a^2+4ab+4b^2=4a^2+4b^2\)
\(\Rightarrow3a^2-4ab=0\Rightarrow\left[{}\begin{matrix}a=0\\3a=4b\end{matrix}\right.\)
Chọn \(\left[{}\begin{matrix}\left(a;b\right)=\left(0;1\right)\\\left(a;b\right)=\left(4;3\right)\end{matrix}\right.\) \(\Rightarrow\) có 2 đường thẳng thỏa mãn: \(\left[{}\begin{matrix}y+3=0\\4x+3y+5=0\end{matrix}\right.\)

Người ra đề chắc hơi lộn xộn một chút về kí hiệu các điểm, vì điểm \(A\left(1;2\right)\) chắc chắn không liên quan gì đến điểm A trong "cắt đường tròn tại 2 điểm AB" (vì một điểm thuộc đường tròn (C) còn 1 điểm thì không)
Để đỡ nhầm lẫn, chúng ta thay tên \(A\left(1;2\right)\) bằng \(M\left(1;2\right)\)
Đường tròn (C) tâm \(I\left(2;-1\right)\) bán kính \(R=2\)
Do \(AB=4=2R\) nên AB là đường kính
\(\Rightarrow\Delta\) đi qua tâm I
\(\overrightarrow{IM}=\left(1;-3\right)\Rightarrow\) đường thẳng \(\Delta\) nhận (3;1) là 1 vtpt
Phương trình \(\Delta\):
\(3\left(x-1\right)+1\left(y-2\right)=0\Leftrightarrow3x+y-5=0\)

Đường tròn (C) tâm \(I\left(-1;0\right)\) bán kính \(R=3\)
\(MN=6=2R\Rightarrow MN\) là đường kính
\(\Rightarrow\) Đường thẳng d đi qua tâm I của đường tròn
\(\Rightarrow\) Đường thẳng d là đường thẳng IA
\(\overrightarrow{IA}=\left(3;3\right)=3\left(1;1\right)\Rightarrow\) đường thẳng d nhận (1;-1) là 1 vtpt
Phương trình d:
\(1\left(x-2\right)-1\left(y-3\right)=0\Leftrightarrow x-y+1=0\)
