Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có :
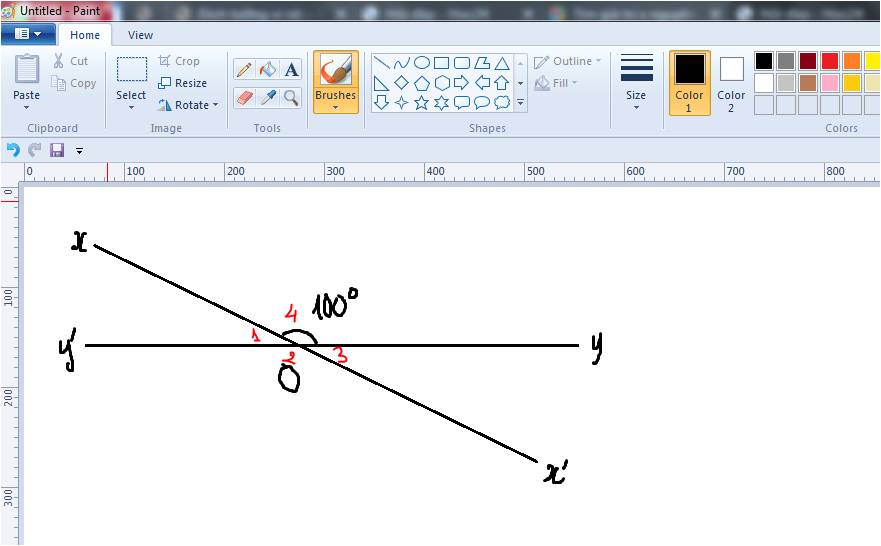
`@)` `\hat{x'Oy'} = \hat{xOy} = 100^@` (hai góc đối đỉnh)
`@)` `\hat{xOy + \hat{xOy'} = 180^@`
hay `100 +` `\hat{xOy'} = 180^@`
`⇒\hat{xOy'} = 180^@ - 100^@ = 80^@`
`@)` `\hat{x'Oy} = \hat{xOy'} = 80^@` (hai góc đối đỉnh)

Vì xx' và yy' là cắt nhau tại A
=> xAy = y'Ax ( đối đỉnh)
Mà xAy + y'Ax = 140°
=> xAy = y'Ax = \(\frac{140°}{2}\)=70°
Mà xAy + yAx' = 180° ( kề bù)
=> yAx' = 180° - 70° = 110°

B1: \(\widehat{yOx'}=180^o-45^o=135^o\)(2 góc kề bù)
\(\widehat{x'Oy'}=45^o\)(đối đỉnh với góc xOy)
\(\widehat{xOy'}=135^o\)(đói đỉnh với góc yOx')
B2: Ta có: Ot và Ot' đối nhau => \(\widehat{tOt'}=180^o\)=>\(\widehat{tOz}=\frac{\widehat{tOt'}}{5}=\frac{180^o}{5}=36^o\)=> \(\widehat{t'Oz}=36^o\)(đối đỉnh với \(\widehat{tOz}\))

Vẽ hai đường thẳng xx" và yy" theo đề bài: góc xOy=x"Oy" =100 độ( Vì đây là hai góc đối đỉnh)
- góc xOy+xOy"=180 độ ( Vì đây là hai góc kề bù) => xOy"+100độ=180độ=> xOy"=180-100=80độ
Do xOy" và x"oy là hai góc đối đỉnh nên xOy"=x"Oy=80độ
Vì xOx" và yOy" là góc bẹt nên xOx"=yOy"=180độ
Vậy xOy=x"Oy"=100độ, xOy"=x"oy=80độ, xOx"=yOy"=180độ

Bài 1:
a: góc xOy'=180-110=70 độ
góc zOy'=70/2=35 độ
góc yOt=góc x'Oy/2=70/2=35 độ
b: Vì góc yOt=góc y'Oz
nên góc y'Oz+góc y'Ot=180 độ
=>Oz và Ot là hai tia đối nhau

a) Các cặp góc kề bù
\(\widehat{xOy}\) và \(\widehat{yOx'}\)
\(\widehat{yOx'}\) và \(\widehat{x'Oy'}\)
\(\widehat{x'Oy'}\) và \(\widehat{xOy'}\)
\(\widehat{xOy'}\) và \(\widehat{xOy}\)
Các cặp góc đối:
\(\widehat{xOy}\) và \(\widehat{x'Oy'}\)
\(\widehat{x'Oy}\) và \(\widehat{y'Ox}\)
b) Do \(\widehat{xOy}\) kề bù với \(\widehat{xOy'}\)
\(\Rightarrow\widehat{xOy}+\widehat{xOy'}=180^o\)
\(\Rightarrow\widehat{xOy'}=180^o-70^o=110^o\)
Ta có :
xAy = 53 độ
+) Ta có :
xAy + yAx' = 180 độ (2 góc kề bù)
Mà xAy = 53 độ
=> 53 +độ + yAx' = 180 độ
=> yAx' = 180 độ - 53 độ
=> yAx' = 127 độ
+) Ta có :
xAy = x'Ay' (đối đỉnh)
Mà xAy = 53 độ
=> x'Ay' = 53 độ
+) Ta có :
yAx' = y'Ax (đối đỉnh)
Mà yAx' = 127 độ
=> y'Ax = 127 độ