

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Ta có: \(a // b\) (GT)
\(\rightarrow \widehat{aAB} = \widehat{bBA}\) (so le trong)
mà \(\widehat{aAx} = \widehat{xAB} = {\widehat{aAB} \over 2}\)(Ax là tia phân giác của \(\widehat{aAB}\))
\(\widehat{bBy} = \widehat{yBA} = {\widehat{bBA} \over 2}\)(By là tia phân giác của \(\widehat{bBA}\))
\(\rightarrow \widehat{ABy} = \widehat{BAx}\)
mà \(\widehat{ABy}\) và \(\widehat{BAx}\) so le trong
\(\rightarrow Ax // By\)
Chúc bạn học tốt..

Hướng dẫn cách làm (nhớ vẽ hình và ghi GT, KL nha):
Từ a//b suy ra 2 góc so le trong bất kì(1) bằng nhau, rồi từ Ax và By là 2 tia phân giác của 2 góc đó rồi suy ra Ax // By vì có cặp góc so le trong tạo bởi 2 góc là nửa của 2 góc so le trong bất kì đó(1)

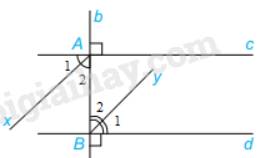
Vì Ax là tia phân giác của góc A vuông nên \(\widehat {{A_1}} = \widehat {{A_2}} = \frac{1}{2}.90^\circ = 45^\circ \)
Vì By là tia phân giác của góc B vuông nên \(\widehat {{B_1}} = \widehat {{B_2}} = \frac{1}{2}.90^\circ = 45^\circ \)
Vì \(\widehat {{A_2}} = \widehat {{B_2}}( = 45^\circ )\), mà hai góc này ở vị trí so le trong nên Ax // By (Dấu hiệu nhận biết hai đường thẳng song song)