Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: \(10^{2k}-1=\left(10^k-1\right)\left(10^k+1\right)⋮9\)
b: \(10^{3k}-1=\left(10^k-1\right)\left(10^{2k}+10^k+1\right)⋮9\)

a,Ta có:\(10^{2k}-1=10^{2k}-10^k+10^k-1=10^k.\left(10^k-1\right)+10^k-1=\left(10^k+1\right)\left(10^k-1\right)\) chia hết cho 9
b,Ta có:
\(10^{3k}-10^{2k}+10^{2k}-10^k+10^k-1=10^{2k}\left(10^k-1\right)+10^k\left(10^k-1\right)+10^k-1\)
\(=\left(10^{2k}+10^k+1\right).\left(10^k-1\right)\) chia hết cho 9

a) \(\overline{ab}+\overline{ba}=10a+b+10b+a=11a+11b=11.\left(a+b\right)\)
Vì 11⋮11 nên \(\overline{ab}+\overline{ba}\)⋮11

a/ 10 ^2k - 1 = 10 ^ 2k - 10 ^k + 10 ^ k -1 = 10 ^k(10 ^ k - 1 ) + ( 10 ^ k - 1 ) chia hết cho 19. Bạn hay xem lại các tính chất
b/ 10^3k -1 = 10 ^ 3k - 10 ^k + 10^ k - 1 = 10 ^ k ( 10^2k - 1 ) + ( 10 ^k - 1) chia hết cho 19. xem lại bài a nha. h
nhớ tick nha

a) 10k - 1 chia hết cho 9 => (10k - 1)(10k + 1) chia hết cho 9 => 102k - 1 chia hết cho 9

Câu 1:
Số tổ nhiều nhất có thể chia là UCLN(24;20)
hay số tổ nhiều nhất có thể chia là 4 tổ
Câu 2:
\(10^{2k}-1=\left(10^k-1\right)\left(10^k+1\right)⋮19\)
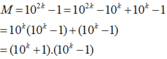
a/ 10 ^2k - 1 = 10 ^ 2k - 10 ^k + 10 ^ k -1 = 10 ^k(10 ^ k - 1 ) + ( 10 ^ k - 1 ) chia hết cho 19. Bạn hay xem lại các tính chất
b/ 10^3k -1 = 10 ^ 3k - 10 ^k + 10^ k - 1 = 10 ^ k ( 10^2k - 1 ) + ( 10 ^k - 1) chia hết cho 19. xem lại bài a nha. h
@@@