Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Áp dụng định luật bảo toàn khối lượng, ta tìm số mol HCl: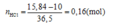
Vì cả 3 amin đều đơn chức nên sẽ phản ứng với HCl theo tỉ lệ mol là 1:1.
Giả sử số mol 3 amin lần lượt là: x; 10x; 5x (mol).
Ta có phương trình:
Giả sử khối lượng mol amin thứ 2 là M(g) ta sẽ có:
amin thứ 2 là: C3H9N 2 amin còn lại là C2H7N, C4H11N
Đáp án B.

Đáp án D.
Vì hỗn hợp amin đơn chức
⇒ ∑nHỗn hợp amin = ∑nHCl pứ = 31 , 68 - 20 36 , 5 = 0,32 mol.
+ Từ tỷ lệ mol 3 amin X, Y và Z
⇒ Số mol 3 nX = 0,02 mol
⇒ nY = 0,2 mol
⇒ nZ = 0,1 mol.
+ Đặt CT của X Y và Z lần lượt là:
R–NH2, R–CH2–NH2, R–(CH2)2–NH2.
⇒ 0,02×(R+16) + 0,2×(R+14+16) + 0,1×(R+28+16) = 20
⇒ R = 29 (C2H5–).
⇒ CTPT của X Y và Z lần lượt là: C2H7N, C3H9N, C4H11N.

m a x i t = m m u o i − m a m i n = 31 , 68 − 20 = 11 , 68 g a m
n H C l = 11 , 68 / 36 , 5 = 0 , 32 m o l
Vì đây là amin đơn chức => n a m i n = n H C l = 0 , 32 m o l
Số mol mỗi amin (theo thứ tự M tăng dần) lần lượt là: 0,02; 0,2 và 0,1
Gọi khối lượng mol của amin có M bé nhất là X (gam/mol)
Vậy M của 2 amin còn lại là: X + 14; X + 28
Ta có phương trình:
0,02 *X + 0,2 * (X + 14) + 0,1 (X + 28) = 20
=> X = 45 => là C 2 H 7 N
Vậy 2 amin còn lại sẽ là: C 3 H 9 N v à C 4 H 11 N
Đáp án cần chọn là: A

Đáp án D
BTKL: mHCl=m muối – m amin = 31,68-20 = 11,68 g => nHCl=0,32 mol=n amin
X: CnH2n+3N: 0,02
Y: Cn+1H2n+5N: 0,2
Z: Cn+2H2n+7N: 0,1
=> 0,02.MX+0,2.(MX+14)+0,1(MX+28)=20=>MX=45 (C2H7N)
Vậy 3 amin là: C2H7N, C3H9N, C4H11N

Đáp án B.
→ B T K L n H C l = 0 , 32 → n a m i n = 0 , 32
số mol 3 amin X; Y; Z lần lượt là 0,02; 0,2; 0,1 mol
![]()
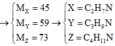

\(m_{HCl}=63,36-40=23,36\left(g\right)\)
=> \(n_{HCl}=\dfrac{23,36}{36,5}=0,64\left(mol\right)\)
=> \(V_{ddHCl}=\dfrac{0,64}{1}=0,64\left(l\right)=640\left(ml\right)\)
=> D

Đáp án : B
Theo bài ra, ta tìm được số mol của 3 chất theo thứ tự lần lượt là 0,02; 0,2:0,1
Gọi chất đầu tiên có M nhỏ nhất
=> 0,32M + 0,2.14 + 0,1.28 = 20 =>M = 45
=> C2H5NH2, C3H7NH2, C4H9NH2
=> Đáp án B