Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\int\limits^1_0\dfrac{xdx}{\left(x+2\right)^2}=\int\limits^1_0\dfrac{1}{x+2}dx-\int\limits^1_0\dfrac{2}{\left(x+2\right)^2}dx=ln\left(x+2\right)|^1_0+\dfrac{2}{x+2}|^1_0=ln3-ln2-\dfrac{1}{3}\)
\(\Rightarrow\left\{{}\begin{matrix}a=-\dfrac{1}{3}\\b=-1\\c=1\end{matrix}\right.\)

Chọn C
Gọi A (d; e; f) thì A thuộc mặt cầu (S1): (x - 1)2 + (y - 2)2 + (z- 3)2 = 1 có tâm I1 = (1; 2; 3), bán kính R1 = 1
B (a; b; c) thì B thuộc mặt cầu (S2): (x - 3)2 + (y - 2)2 + z2 = 9 có tâm I2 = (-3; 2; 0), bán kính R2 = 3
Ta có I1I2 = 5 > R1 + R2 => (S1) và (S2) không cắt nhau và ở ngoài nhau.
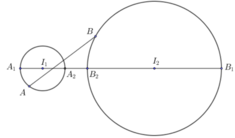
Dễ thấy F = AB, AB max khi A ≡ A1; B ≡ B1
=> Giá trị lớn nhất bằng I1I2 + R1 + R2 = 9.
AB min khi A ≡ A2; B ≡ B2
=> Giá trị nhỏ nhất bằng I1I2 - R1 - R2 = 1.
Vậy M - m =8

\(I=\int e^xcosxdx\Rightarrow\left\{{}\begin{matrix}u=cosx\\dv=e^xdx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=-sinx.dx\\v=e^x\end{matrix}\right.\)
\(\Rightarrow I=e^xcosx+\int e^xsinx.dx=e^xcosx+I_1\)
\(I_1=\int e^xsinx\Rightarrow\left\{{}\begin{matrix}u=sinx\\dv=e^xdx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=cosx.dx\\v=e^x\end{matrix}\right.\)
\(\Rightarrow I_1=e^xsinx-\int e^xcosx.dx=e^x.sinx-I\)
\(\Rightarrow I=e^xcosx+e^xsinx-I\Rightarrow2I=e^x\left(cosx+sinx\right)\)
\(\Rightarrow I=e^x\left(\frac{1}{2}cosx+\frac{1}{2}sinx\right)+C\Rightarrow\left\{{}\begin{matrix}A=\frac{1}{2}\\B=\frac{1}{2}\end{matrix}\right.\)
\(\Rightarrow A+B=1\)

Câu 1: Là \(ln^2x+lnx\) hay \(lnx^2+lnx\) bạn, hai cái này khác nhau lắm, viết thế kia chẳng hiểu gì cả. Biểu thức logarit nếu viết mũ, thì hoặc là viết thế này \(ln^2x\) hoặc là \(\left(lnx\right)^2\), nếu viết \(ln\left(x\right)^2\) người ta sẽ mặc định hiểu là \(ln\left(x^2\right)\)
Chắc là cái đầu, vậy ta biến đổi được:
\(lnx\left(lnx+1\right)=lnx\left(lnx+lne\right)=lnx.ln\left(x.e\right)=ln\left(x.e\right)^{lnx}\)
Câu 2: đạo hàm 4 cái ra, dễ dàng nhận ra ở đáp án d, với \(x\ge0\Rightarrow f'\left(x\right)=3x^2+4x+\frac{1}{2\sqrt{x}}>0\) luôn đồng biến nên hàm không có cực trị
Câu 3:
Phương trình hoành độ giao điểm:
\(\frac{m-x}{x+1}=2x+m\Leftrightarrow m-x=2x^2+\left(m+2\right)x+m\)
\(\Leftrightarrow2x^2+\left(m+3\right)x=0\)
Phương trình luôn có nghiệm \(x=0\) hay ít nhất 1 trong 2 điểm A; B sẽ trùng gốc tọa độ tức \(OA=0\) hoặc \(OB=0\)
Do đó ko tồn tại m thỏa mãn
Câu 4:
\(\left\{{}\begin{matrix}lnx=X\\lny=Y\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}2X^2+3Y^2=5\\X+4Y=3\end{matrix}\right.\)
\(\Rightarrow2\left(3-4Y\right)^2+3Y^2=5\)
\(\Leftrightarrow35Y^2-48Y+13=0\Rightarrow\left[{}\begin{matrix}Y=1\Rightarrow X=-1\\Y=\frac{13}{35}\Rightarrow X=\frac{53}{35}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}lnx=-1\\lny=1\end{matrix}\right.\) \(\Rightarrow\left(x;y\right)=\left(e^{-1};e\right)\) \(\Rightarrow\left\{{}\begin{matrix}c=-1\\d=1\end{matrix}\right.\)
Hoặc \(\left\{{}\begin{matrix}lnx=\frac{53}{35}\\lny=\frac{13}{35}\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=e^{\frac{53}{35}}=e\sqrt[35]{e^{18}}\\y=e^{\frac{13}{35}}=\sqrt[35]{e^{13}}\end{matrix}\right.\) \(\Rightarrow a=b=35\)
Đáp án b sai
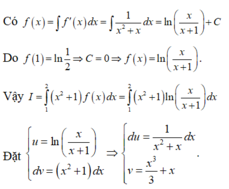
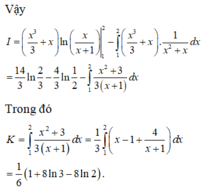
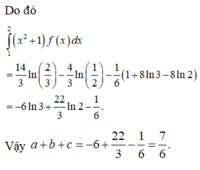
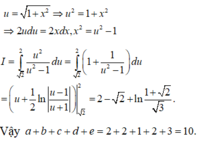
Chọn đáp án B. Đặt