
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

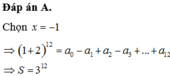

a/ \(-12\left(x-5\right)+7\left(3-x\right)=5\)
\(< =>-12x+60+21-7x=5\)
\(< =>-19x+81=5\)
\(< =>-19x=-76\)
\(< =>x=\frac{76}{19}\)
b/ 30(x+2)-6(x-5)-24x=100
<=>30x + 60 - 6x + 30 - 24x =100
<=> 90=100( vô lý)
c/ \(\left(x-1\right)\left(x^2+1\right)=0\)
\(< =>\hept{\begin{cases}x-1=0\\x^2+1=0\end{cases}}< =>\hept{\begin{cases}x=1\\x^2=-1\left(voly\right)\end{cases}}\)
d/ làm rồi mà
a. \(-12.\left(x-5\right)+7.\left(3-x\right)=5\)
\(-12x+60+21-7x=5\)
\(-19x+81=5\)
\(-19x=-76\)
\(x=4\)
b. \(30.\left(x+2\right)-6.\left(x-5\right)-24x=100\)
\(30x+60-6x+30-24x=100\)
\(\left(30x-6x-24x\right)+\left(60+30\right)=100\)
\(90=100\)(vô lí)
\(\Rightarrow x=\varnothing\)
c. \(\left(x-1\right)\left(x^2+1\right)=0\)
\(\Rightarrow\orbr{\begin{cases}x-1=0\\x^2+1=0\end{cases}\Rightarrow\orbr{\begin{cases}x=1\\x^2=-1\left(loại\right)\end{cases}}}\)
\(\Rightarrow x=1\)
Câu d) chính là câu a) :D

1.
Đặt \(\sqrt[12]{a}=x\ge0\)
\(\Rightarrow VT=2^x+2^{x^3}\ge2\sqrt{2^{x+x^3}}\ge2\) (đpcm)
Dấu "=" xảy ra khi \(x=0\) hay \(a=0\)
2.
\(y=2^{x-1}+2^{3-x}\ge2\sqrt{2^{x-1+3-x}}=4\)
\(y_{min}=4\) khi \(x-1=3-x\Leftrightarrow x=2\)

Đáp án A
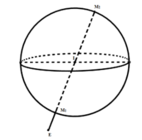
Mặt cầu (S) có tâm I(1;1;1). Gọi E là điểm thoả mãn
![]()
![]()
T nhỏ nhất khi ME nhỏ nhất <=> M là 1 trong 2 giao điểm của đường thẳng IE và mặt cầu (S).
![]()
![]()
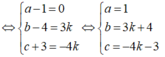
![]()
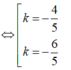
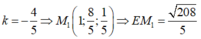
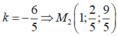
![]()
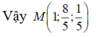

Đáp án: B.
Các phương trình còn lại có nhiều hơn một nghiệm:
(x - 5)( x 2 - x - 12) = 0 có các nghiệm x = 5, 4, -3.
sin 2 x - 5sinx + 4 = 0 ⇔ sinx = 1, có vô số nghiệm
sinx - cosx + 1 = 0 có các nghiệm x = 0, x = 3 π /2

Đáp án: B.
Các phương trình còn lại có nhiều hơn một nghiệm:
(x - 5)( x 2 - x - 12) = 0 có các nghiệm x = 5, 4, -3.
sin 2 x - 5sinx + 4 = 0 ⇔ sinx = 1, có vô số nghiệm
sinx - cosx + 1 = 0 có các nghiệm x = 0, x = 3π/2.