Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\Delta\)EAC đông dạng EBD
=> k = EA / EB = AC / BD = R/2 / ( 2R+R/2) = 1/5

a, (O, R) có EM là tiếp tuyến ( M là tiếp điểm)
=> OM= R, EM\(\perp\)OM tại M
(O, R) có AB là đk
=> O là TĐ của AB
=> OA=OB=1/2AB=R
Tam giác AMB có MO là đường trung tuyến ứng với AB, MO=R=1/2AB
=> Tam giác AMB vuông tại M
C/ M các tiếp tuyến AC, CM cắt nhau => AC=CM
BD, MD cắt nhau => BD=MD
=> AC+BD=CM+MD=CD
b, Có OA=OM=R, AC=CM
=> OC là đường trung trực của AM
Mà OC cắt AM tại H
=> OC vuông với AM tại H, H là TĐ của AM.
C/M T.T: OD vuông với MB tại K, K là TĐ của MB.
T/g OKMH có 3 góc vuông AMB, OHM, OKM nên là hcn
c, DO là p/g góc MDB => MDO=ODB=1/2 MDB
OBD=90=> OBK+KBD=90
Tam giác DKB vuông tại K=> KBD+BDK=90
=> BDK=OBK
mà BDK=ODM=> OBK=ODM => ABM=ODC
C/m OC, OD lần lượt là p/g AOM, MOB . Từ đó c/m COD=90
C/m Tam giác ABM đồng dạng với tam giác CDO (gg)
=> AM/CO=BM/DO
=> AM.DO=MB.CO

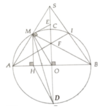
a, Chứng minh ∆MEF:∆MOA
b, ∆MEF:∆MOA mà AO=OM => ME=EF
c, Chứng minh F là trực tâm của ∆SAB, AI là đường cao, chứng minh A,I,F thẳng hàng
d, FA.SM = 2 R 2
e, S M H O = 1 2 OH.MH ≤ 1 2 . 1 2 M O 2 = 1 4 R 2
=> M ở chính giữa cung AC
ta có: EM = \(\sqrt{OE^2-OM^2}=\sqrt{4R^2-R^2}=\sqrt{3}R.\)
(pytago)
xét tg vuông EOM và EDB có: góc E chung => 2 tam giác đồng dạng
=> \(\frac{EM}{OE}=\frac{EB}{ED}\Leftrightarrow ED=\frac{EB.OE}{EM}=\frac{2R.3R}{\sqrt{3}R}=2\sqrt{3}R\)
lại có: BD=\(\sqrt{ED^2-BE^2}=\sqrt{12R^2-9R^2}=\sqrt{3}R\)
(pytago)
xét tg vuông EAC và EBD có E chung => 2 tg đồng dạng
=>\(\frac{EA}{EB}=\frac{AC}{BD}\Leftrightarrow AC=\frac{EA.BD}{EB}=\frac{R.\sqrt{3}R}{3R}=\frac{R}{\sqrt{3}}\)
\(S_{ABDC}=\frac{\left(AC+DB\right).AB}{2}=\frac{\left(\frac{R}{\sqrt{3}}+\sqrt{3}R\right).2R}{2}=\left(3+\sqrt{3}\right).R^2\)
cảm ơn