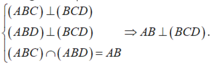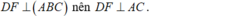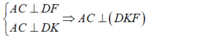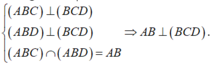Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: AM vuông góc BD
=>AM vuông góc (BCD)
b: Kẻ DK vuông góc BC
=>BK vuông góc BC
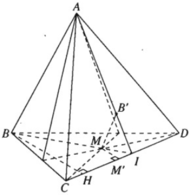
(ABD) vuông góc (BCD)
=>DK vuông góc BA
=>(BCD) vuông góc (ABC)
c: AN là giao tuyến chung của (ABC) và (ANM)
=>MH vuông góc AN
=>MH vuông góc (ABC)

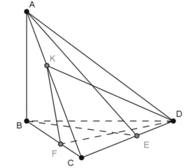
a) MB' qua M và song song với (ABC) và (ABD) ⇒ MB′ song song với giao tuyến AB của hai mặt phẳng này. Ta có: MB′ // AB nên MB' và AB xác định một mặt phẳng. Giả sử MB cắt AB' tại I.
Ta có: I ∈ BM ⇒ I ∈ (BCD)
I ∈ AB′ ⇒ I ∈ (ACD)
Nên I ∈ (BCD) ∩ (ACD) = CD
Có: I ∈ CD
Vậy ba đường thẳng AB', BM và CD đồng quy tại I.
b) MB′ // AB 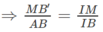
Kẻ MM′ ⊥ CD và BH ⊥ CD
Ta có: MM′ // BH 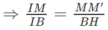
Mặt khác:
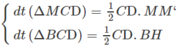
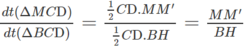
Do đó: 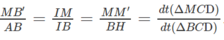
Vậy 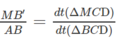
c) Tương tự ta có: 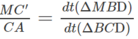
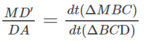
Vậy:
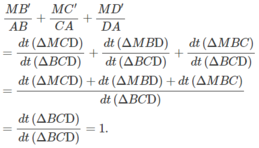


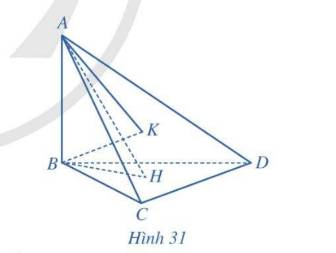
a) Xét tam giác ABC cân tại A có
I là trung điểm của BC
\( \Rightarrow AI \bot BC\)
Xét tam giác ACD cân tại D có
I là trung điểm của BC
\( \Rightarrow DI \bot BC\)
Ta có \(AI \bot BC,DI \bot BC \Rightarrow BC \bot \left( {AID} \right)\)
b) \(BC \bot \left( {AID} \right);BC \subset \left( {BCD} \right) \Rightarrow \left( {BCD} \right) \bot \left( {AID} \right)\)
\(\left( {BCD} \right) \cap \left( {AID} \right) = DI\)
Trong (AID) có \(AH \bot DI\)
\( \Rightarrow AH \bot \left( {BCD} \right)\)
c) Ta có \(BC \bot \left( {AID} \right);IJ \subset \left( {AID} \right) \Rightarrow BC \bot IJ\)
Mà \(IJ \bot AD\)
Do đó IJ là đường vuông góc chung của AD và BC.

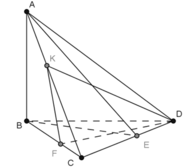
a) Vì \(AB \bot \left( {BCD} \right) \Rightarrow AB \bot CD\left( 1 \right)\)
Có H là trực tâm của tam giác BCD \( \Rightarrow BH \bot CD\left( 2 \right)\)
Tử (1) và (2) \( \Rightarrow CD \bot \left( {ABH} \right)\)
b) Vì \(AB \bot \left( {BCD} \right) \Rightarrow AB \bot CD\left( 1 \right)\)
Có K là trực tâm của tam giác BCD \( \Rightarrow AK \bot CD\left( 2 \right)\)
Từ (1) và (2) \( \Rightarrow CD \bot \left( {ABK} \right)\)