
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Để phương trình có nghiệm thì: m2≠0 =>m≠0
b) Vì phương trình có nghiệm bằng -2m
=>-(m+2)2m-m2=0 ⇔-2m2-4m-m2=0 ⇔-3m2-4m=0 ⇔-m(3m+4)=0
⇔m=0 hay m=\(\dfrac{-4}{3}\)mà m phải khác 0 nên m=\(\dfrac{-4}{3}\).
c) -(m+2)x-m2=0 ⇔x=\(\dfrac{m^2}{m+2}\)>0 ⇔m+2>0 ⇔m>-2.
d) -(m+2)x-m2=0 ⇔x=\(\dfrac{m^2}{m+2}\).
Để x nguyên thì m2 ⋮ m+2.
⇔ m2-4+4 ⋮ m+2
⇔ 4 ⋮ m+2
⇔ m∈{-1;-3;0;-4;2;-6} mà m khác 0 nên m∈{-1;-3;-4;2;-6}

Ta có:
\(3x-3=3\left(x-1\right)\)
\(4-4x=-4\left(x-1\right)\)
\(x^2-1=\left(x-1\right)\left(x+1\right)\)
\(\Rightarrow\) MTC là \(3.\left(-4\right).\left(x-1\right)\left(x+1\right)=-12\left(x-1\right)\left(x+1\right)\)
Do đó:
\(\dfrac{11x}{3x-3}=\dfrac{11x}{3\left(x-1\right)}=\dfrac{11x.\left(-4\right).\left(x+1\right)}{3\left(x-1\right).\left(-4\right)\left(x+1\right)}=\dfrac{-44x\left(x+1\right)}{-12\left(x-1\right)\left(x+1\right)}\)
\(\dfrac{5}{4-4x}=\dfrac{5}{-4\left(x-1\right)}=\dfrac{5.3\left(x+1\right)}{-4\left(x-1\right).3\left(x+1\right)}=\dfrac{15\left(x+1\right)}{-12\left(x-1\right)\left(x+1\right)}\)
\(\dfrac{2x}{x^2-1}=\dfrac{2x}{\left(x-1\right)\left(x+1\right)}=\dfrac{2x.\left(-12\right)}{-12\left(x-1\right)\left(x+1\right)}=\dfrac{-24x}{-12\left(x-1\right)\left(x+1\right)}\)

a: Xét ΔKAB và ΔKCD có
\(\widehat{KAB}=\widehat{KCD}\)(hai góc so le trong, AB//CD)
\(\widehat{AKB}=\widehat{CKD}\)(hai góc đối đỉnh)
Do đó: ΔKAB đồng dạng với ΔKCD
=>\(\dfrac{KA}{KC}=\dfrac{KB}{KD}\)
=>\(KA\cdot KD=KB\cdot KC\)
b: Ta có: \(\dfrac{KA}{KC}=\dfrac{KB}{KD}\)
=>\(\dfrac{KC}{KA}=\dfrac{KD}{KB}\)
=>\(\dfrac{KC}{KA}+1=\dfrac{KD}{KB}+1\)
=>\(\dfrac{KC+KA}{KA}=\dfrac{KD+KB}{KB}\)
=>\(\dfrac{AC}{KA}=\dfrac{BD}{KB}\)
=>\(\dfrac{AK}{AC}=\dfrac{BK}{BD}\left(1\right)\)
Xét ΔADC có IK//DC
nên \(\dfrac{AK}{AC}=\dfrac{IK}{DC}\left(2\right)\)
Xét ΔBDC có KQ//DC
nên \(\dfrac{KQ}{DC}=\dfrac{BK}{BD}\left(3\right)\)
Từ (1),(2),(3) suy ra IK=KQ

a: ĐKXĐ: \(x\notin\left\{10;-10;\sqrt{10};-\sqrt{10}\right\}\)
b: \(A=\dfrac{5x^3+50x+2x^2+20+5x^3-50x-2x^2+20}{\left(x^2-10\right)\left(x^2+10\right)}\cdot\dfrac{x^2-100}{x^2+4}\)
\(=\dfrac{10x^3+40}{\left(x^2-10\right)\left(x^2+10\right)}\cdot\dfrac{x^2-100}{x^2+4}\)

a: \(=5x^2-10x-5x^2+7x=-3x\)
b: \(=2x^3+3xy^2-4y-3xy^2=2x^3-4y\)

a) \(\dfrac{2\left(x-2\right)}{x\left(x-2\right)}=\dfrac{2}{x}\)
\(a,=\dfrac{2\left(x-2\right)}{x\left(x-2\right)}=\dfrac{2}{x}\\ b,=\dfrac{\left(1-3x\right)\left(2x-1\right)+2x\left(3x-2\right)-\left(3x-2\right)}{2x\left(2x-1\right)}\\ =\dfrac{\left(1-3x\right)\left(2x-1\right)+\left(2x-1\right)\left(3x-2\right)}{2x\left(2x-1\right)}\\ =\dfrac{\left(2x-1\right)\left(1-3x+3x-2\right)}{2x}=\dfrac{-1}{2x}\)

Lời giải:
$(2x-3)(x^2+1)=0$
\(\Leftrightarrow \left[\begin{matrix} 2x-3=0\\ x^2+1=0\end{matrix}\right.\Leftrightarrow \left[\begin{matrix} x=\frac{3}{2}(\text{chọn})\\ x^2=-1<0(\text{vô lý})\end{matrix}\right.\)
Vậy pt có nghiệm $x=\frac{3}{2}$

\(\dfrac{2}{x+1}-\dfrac{1}{x-2}=\dfrac{3x-11}{\left(x+1\right)\left(x-2\right)}\\ \Leftrightarrow\dfrac{2.\left(x-2\right)}{\left(x+1\right)\left(x-2\right)}-\dfrac{1.\left(x+1\right)}{\left(x+1\right)\left(x-2\right)}=\dfrac{3x-11}{\left(x+1\right)\left(x-2\right)}\\ \Leftrightarrow2x-4-x+1=3x-11\\ \Leftrightarrow x-3=3x-11\\ \Leftrightarrow x-3x=-11+3\\ \Leftrightarrow-2x=-8\\ \Leftrightarrow x=4\)
Vậy tập nghiệm của phương trình là S = { 4 }
 ạ vì mình ko hiểu ạ
ạ vì mình ko hiểu ạ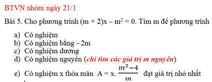


 Các bạn giải giúp mình với ạ, phần a ghi chi tiết bước giải hộ mình nhé. Mình cám ơn ạ! (Mai mình nộp rồi nên nhanh giúp mình ạ T.T)
Các bạn giải giúp mình với ạ, phần a ghi chi tiết bước giải hộ mình nhé. Mình cám ơn ạ! (Mai mình nộp rồi nên nhanh giúp mình ạ T.T)
ko bt
a: \(Q=\dfrac{2x^2-4x+x-3-6}{\left(x-3\right)\left(x-2\right)}\cdot\dfrac{x-2}{x^2+1}=\dfrac{2x^2-3x-9}{x-3}\cdot\dfrac{1}{x^2+1}\)
\(=\dfrac{2x^2-6x+3x-9}{x-3}\cdot\dfrac{1}{x^2+1}=\dfrac{2x+3}{x^2+1}\)
b: Để Q>0 thì 2x+3>0
hay x>-3/2