
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 1:
Vận tốc cano khi dòng nước lặng là: $25-2=23$ (km/h)
Bài 2:
Đổi 1 giờ 48 phút = 1,8 giờ
Độ dài quãng đường AB: $1,8\times 25=45$ (km)
Vận tốc ngược dòng là: $25-2,5-2,5=20$ (km/h)
Cano ngược dòng từ B về A hết:
$45:20=2,25$ giờ = 2 giờ 15 phút.

Bài 1:
a.
$a^3-a^2c+a^2b-abc=a^2(a-c)+ab(a-c)$
$=(a-c)(a^2+ab)=(a-c)a(a+b)=a(a-c)(a+b)$
b.
$(x^2+1)^2-4x^2=(x^2+1)^2-(2x)^2=(x^2+1-2x)(x^2+1+2x)$
$=(x-1)^2(x+1)^2$
c.
$x^2-10x-9y^2+25=(x^2-10x+25)-9y^2$
$=(x-5)^2-(3y)^2=(x-5-3y)(x-5+3y)$
d.
$4x^2-36x+56=4(x^2-9x+14)=4(x^2-2x-7x+14)$
$=4[x(x-2)-7(x-2)]=4(x-2)(x-7)$
Bài 2:
a. $(3x+4)^2-(3x-1)(3x+1)=49$
$\Leftrightarrow (3x+4)^2-[(3x)^2-1]=49$
$\Leftrightarrow (3x+4)^2-(3x)^2=48$
$\Leftrightarrow (3x+4-3x)(3x+4+3x)=48$
$\Leftrightarrow 4(6x+4)=48$
$\Leftrightarrow 6x+4=12$
$\Leftrightarrow 6x=8$
$\Leftrightarrow x=\frac{4}{3}$
b. $x^2-4x+4=9(x-2)$
$\Leftrightarrow (x-2)^2=9(x-2)$
$\Leftrightarrow (x-2)(x-2-9)=0$
$\Leftrightarrow (x-2)(x-11)=0$
$\Leftrightarrow x-2=0$ hoặc $x-11=0$
$\Leftrightarrow x=2$ hoặc $x=11$
c.
$x^2-25=3x-15$
$\Leftrightarrow (x-5)(x+5)=3(x-5)$
$\Leftrightarrow (x-5)(x+5-3)=0$
$\Leftrightarrow (x-5)(x+2)=0$
$\Leftrightarrow x-5=0$ hoặc $x+2=0$
$\Leftrightarrow x=5$ hoặc $x=-2$

Bài 3:
Gọi x(m) là chiều rộng của mảnh đất(Điều kiện: x>0)
Chiều dài của mảnh đất là: x+5(m)
Theo đề, ta có phương trình:
2x+5=25
\(\Leftrightarrow2x=20\)
hay x=10(thỏa ĐK)
Vậy: Diện tích của mảnh đất là 150m2

"Làm hộ em với ạ, không cần vẽ hình, trình bày đủ là được. Em cảm ơn nhiều!"
?????????
Thiếu đề bn ey ~.~

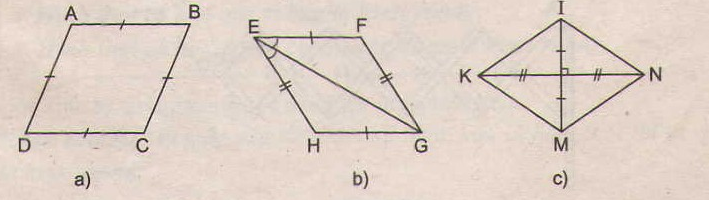
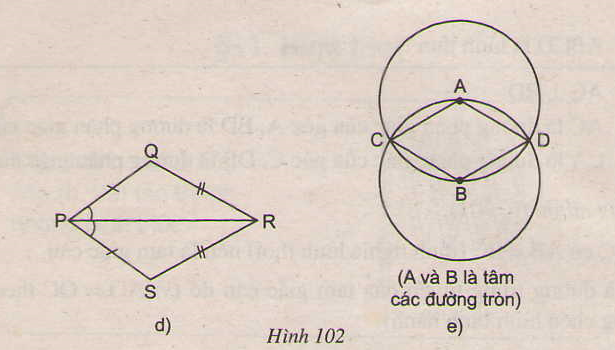
73. Tìm các hình thoi trên hình 102.
Bài giải:
Các tứ giác ở hình 39 a, b, c, e là hình thoi.
- Ở hình 102a, ABCD là hình thoi (theo định nghĩa)
- Ở hình 102b, EFGH là hình thoi (theo dấu hiệu nhận biết 4)
- Ở hình 102c, KINM là hình thoi (theo dấu hiệu nhận biết 3)
-Ở hình 102e, ADBC là hình thoi (theo định nghĩa, vì AC = AD = AB = BD = BC)
Tứ giác trên hình 102d không là hình thoi.
Các tứ giác ở hình 39 a, b, c, e là hình thoi.
- Ở hình 102a, ABCD là hình thoi (theo định nghĩa)
- Ở hình 102b, EFGH là hình thoi (theo dấu hiệu nhận biết 4)
- Ở hình 102c, KINM là hình thoi (theo dấu hiệu nhận biết 3)
-Ở hình 102e, ADBC là hình thoi (theo định nghĩa, vì AC = AD = AB = BD = BC)
Tứ giác trên hình 102d không là hình thoi.

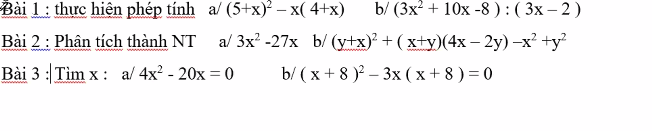



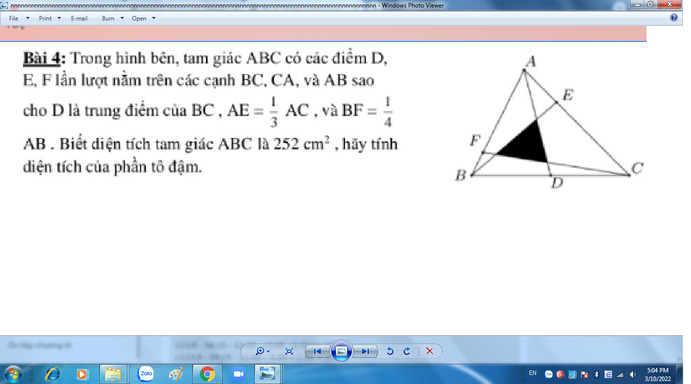





 Mọi Người giải giúp em ạ em cảm ơn ạ
Mọi Người giải giúp em ạ em cảm ơn ạ 
 Làm hộ em với ạ, không cần vẽ hình, trình bày đủ là được. Em cảm ơn nhiều!
Làm hộ em với ạ, không cần vẽ hình, trình bày đủ là được. Em cảm ơn nhiều!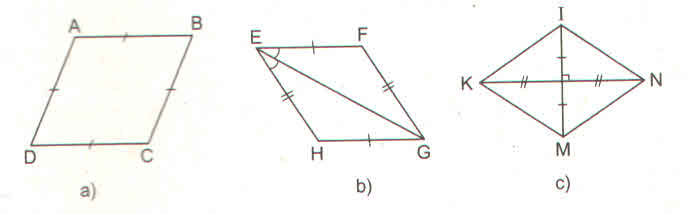

 cd
cd
Bài 2:
\(b,=\left(x+y\right)^2+2\left(2x-y\right)\left(x+y\right)+\left(2x-y\right)^2-4x^2+4xy-y^2-x^2+y^2\\ =\left(x+y+2x-y\right)^2-5x^2+4xy\\ =9x^2-4x^2+4xy=5x^2+4xy=x\left(5x+4y\right)\)