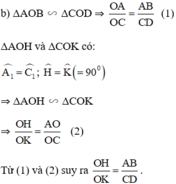Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

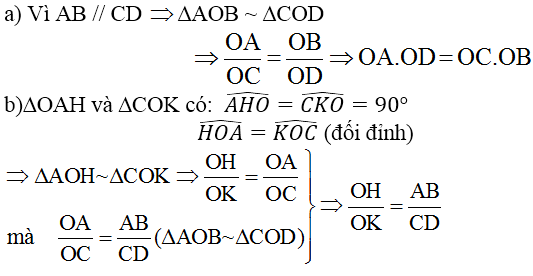
a;Vì AB//CD nên theo định lí Ta-lét ta có:
OA/OC=OB/ODOAOC=OBOD
⇒OA.OD=OC.OB⇒OA.OD=OC.OB
b;Xét ΔAOHΔAOH và ΔCOKΔCOKcó:
AHOˆ=CKO=90oˆAHO^=CKO=90o^
AOHˆ=COKˆAOH^=COK^ (hai góc đối đỉnh)
⇒ΔAOH ΔCOK(g.g)⇒ΔAOH ΔCOK(g.g)
⇒OAOC=OHOK(1)⇒OAOC=OHOK(1)
Vì AB//CD nên theo hệ quả của định lí Ta-lét ta có
ABCD=OAOC(2)ABCD=OAOC(2)
Từ 1 và 2 ta có:
OHOK=ABCD

a;Vì AB//CD nên theo định lí Ta-lét ta có:
\(\dfrac{OA}{OC}=\dfrac{OB}{OD}\)
\(\Rightarrow OA.OD=OC.OB\)
b;Xét \(\Delta AOH\) và \(\Delta COK\)có:
\(\widehat{AHO}=\widehat{CKO=90^o}\)
\(\widehat{AOH}=\widehat{COK}\) (hai góc đối đỉnh)
\(\Rightarrow\Delta AOH~\Delta COK\left(g.g\right)\)
\(\Rightarrow\dfrac{OA}{OC}=\dfrac{OH}{OK}\left(1\right)\)
Vì AB//CD nên theo hệ quả của định lí Ta-lét ta có
\(\dfrac{AB}{CD}=\dfrac{OA}{OC}\left(2\right)\)
Từ 1 và 2 ta có:
\(\dfrac{OH}{OK}=\dfrac{AB}{CD}\)

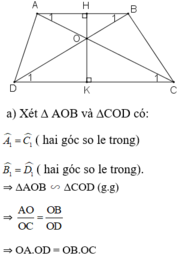
a, Xét 2 tam giác : AOB và COD
\(\widehat{A_1}=\widehat{C_1}\)( 2 góc so le trong )
\(\widehat{B_1}=\widehat{D_1}\)( 2 góc so le trong )
\(\Rightarrow\Delta AOB~\Delta COD\left(gg\right)\)
\(\Rightarrow\frac{AO}{OC}=\frac{OB}{OD}\)
\(\Rightarrow AO.OD=OC.OB\)
b, \(\Delta AOB~\Delta COD\Rightarrow\frac{OA}{OC}=\frac{AB}{CD}\left(1\right)\)
\(\Delta AOH\)và \(\Delta COK\)có :
\(\Rightarrow\frac{OH}{OK}=\frac{AO}{OC}\left(2\right)\)
Từ (1)(2) => \(\frac{OH}{OK}=\frac{AB}{CD}\)

a) Xét ΔAOB và ΔCOD có
\(\widehat{AOB}=\widehat{COD}\)(hai góc đối đỉnh)
\(\widehat{BAO}=\widehat{DCO}\)(hai góc so le trong, AB//DC)
Do đó: ΔAOB∼ΔCOD(g-g)
Suy ra: \(\dfrac{OA}{OC}=\dfrac{OB}{OD}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(OA\cdot OD=OB\cdot OC\)(đpcm)

a: XétΔOAB và ΔOCD có
góc OAB=góc OCD
góc AOB=góc COD
=>ΔOAB đồng dạng với ΔOCD
b: OE là phân giác của góc COD trong ΔCOD
nên EC/ED=OC/OD=OA/OB

a. ta có: AB//CD ( gt )
Áp dụng hệ quả Ta-lét, ta có:
\(\dfrac{ID}{IB}=\dfrac{IC}{IA}\)
\(\Leftrightarrow IA.ID=IB.IC\)
b. xét tam giác IHA và tam giác IKD có : AH // HD
\(\Rightarrow\dfrac{IH}{IK}=\dfrac{AH}{CK}\) ( ta-lét )
xét tam giác IHB và tam giác IKC có: BH // HC
\(\Rightarrow\dfrac{IH}{IK}=\dfrac{BH}{DK}\) ( ta-lét )
\(\Rightarrow\dfrac{IH}{IK}=\dfrac{AH}{CK}=\dfrac{BH}{DK}\Leftrightarrow\dfrac{IH}{IK}=\dfrac{AH+BH}{CK+DK}\) ( t. chất dãy tỉ số = nhau )
\(\Leftrightarrow\dfrac{IH}{IK}=\dfrac{AB}{CD}\) ( AH+BH = AB; CK + DK = CD )
b, Theo hệ quả Ta lét \(\dfrac{AB}{CD}=\dfrac{AI}{IC}\)(*)
Xét tam giác HIA và tam giác KIC có
^HIA = ^KIC (đối đỉnh)
^IHA = ^IKC = 900
Vậy tam giác HIA ~ tam giác KIC (g.g)
\(\Rightarrow\dfrac{IH}{KI}=\dfrac{AI}{IC}\)(**)
Từ (*) ; (**) suy ra \(\dfrac{IH}{KI}=\dfrac{AB}{CD}\)