Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Để \(AC\perp BD\) thì \(\Rightarrow\overrightarrow{AC}\cdot\overrightarrow{BD}=0\Rightarrow\left(\overrightarrow{AB}+\overrightarrow{BC}\right)\left(\overrightarrow{BA}+\overrightarrow{AD}\right)=0\\ \Rightarrow\overrightarrow{AB}\cdot\overrightarrow{BA}+\overrightarrow{BC}\cdot\overrightarrow{BA}+\overrightarrow{AB}\cdot\overrightarrow{AD}+\overrightarrow{BC}\cdot\overrightarrow{AD}=0\\ \Rightarrow-h^2+0+0+ab=0\\ \Rightarrow h^2=ab\)
b) Để \(AI\perp BI\) thì \(\Rightarrow\overrightarrow{AI}\cdot\overrightarrow{BI}=0\Rightarrow\dfrac{1}{2}\left(\overrightarrow{AD}+\overrightarrow{AC}\right)\dfrac{1}{2}\left(\overrightarrow{BD}+\overrightarrow{BC}\right)=0\\ \Rightarrow\left(\overrightarrow{AD}+\overrightarrow{AB}+\overrightarrow{BC}\right)\left(\overrightarrow{BA}+\overrightarrow{AD}+\overrightarrow{BC}\right)=0\\ \\ \Rightarrow\overrightarrow{AD}\cdot\overrightarrow{BA}+\overrightarrow{AB}\cdot\overrightarrow{BA}+\overrightarrow{BC}\cdot\overrightarrow{BA}+\overrightarrow{AD}\cdot\overrightarrow{AD}+\overrightarrow{AB}\cdot\overrightarrow{AD}+\overrightarrow{BC}\cdot\overrightarrow{AD}+\overrightarrow{AD}\cdot\overrightarrow{BC}+\overrightarrow{AB}\cdot\overrightarrow{BC}+\overrightarrow{BC}\cdot\overrightarrow{BC}=0\\ \Rightarrow-h^2+a^2+ab+ab+b^2=0\\ \Rightarrow a^2+2ab+b^2=\left(a+b\right)^2=h^2\\ \Rightarrow a+b=h\)

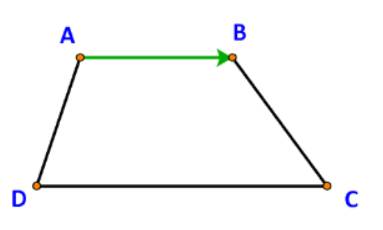
Giá của vectơ \(\overrightarrow {AB} \) là đường thẳng AB.
Các vectơ cùng phương với vectơ \(\overrightarrow {AB} \) là: \(\overrightarrow {CD} \) và \(\overrightarrow {DC} \)
a) vectơ \(\overrightarrow {DC} \) cùng hướng với vectơ \(\overrightarrow {AB} \).
b) vectơ \(\overrightarrow {CD} \) ngược hướng với vectơ \(\overrightarrow {AB} \).

a: Xét ΔCDE vuông tại D và ΔCAB vuông tại A có
góc ACB chung
Do dó ΔCDE đồng dạng với ΔCAB
=>CD/CA=CE/CB
=>CD/CE=CA/CB
=>ΔCDA đồng dạng với ΔCEB
=>EB/DA=BC/AC
mà BC/AC=AC/CH
nên EB/DA=AC/CH=BA/HA
=>BE/AD=BA/HA
=>\(BE=\dfrac{AB}{AH}\cdot AD=\dfrac{AB}{AH}\cdot\sqrt{AH^2+HD^2}\)
\(=\dfrac{AB}{AH}\cdot\sqrt{AH^2+AH^2}=AB\sqrt{2}\)
b: Xét ΔABE vuông tại A có sin AEB=AB/BE=1/căn 2
nên góc AEB=45 độ
=>ΔABE vuông cân tại A
=>AM vuông góc với BE
BM*BE=BA^2
BH*BC=BA^2
Do đó: BM*BE=BH/BC
=>BM/BC=BH/BE
=>ΔBMH đồng dạng với ΔBCE

a)Xét tam giác ACD và tam giác ECD(đều là vuông)![]()
ECD=DCA(Vì CD là p/giác)
CD là cạnh chung
\(\Rightarrow\)tam giác ACD=tam giác ECD(cạnh huyền góc nhọn)
b)Vì tam giác ACD=tam giác ECD(cạnh huyền góc nhọn)
\(\Rightarrow\)AD=DE(cạnh cặp tương ứng)
\(\Rightarrow\)D cách đều hai mút của AE
\(\Rightarrow\)CD là đường trung trực của AE
Do đó CI\(\perp\)AE
\(\Rightarrow\)Tam giác CIE là tam giác vuông
c)Vì AD=DE(câu b)
Mà tam giác BDE là tam giác vuông(tại E)
\(\Rightarrow\)DE<BD(cạnh góc vuông nhỏ hơn cạnh huyền)
\(\Rightarrow\)AD<BD(đpcm)
d)Kéo dài BK cắt AC tại O
Vì BK\(\perp\)CD(gt)
\(\Rightarrow\)CK là đường cao thứ nhất của tam giác OBC(1)
Vì tam giác ABC vuông tại A
Nên BA\(\perp\)AC
\(\Rightarrow\)BA là đường cao thứ hai của tam giác OBC(2)
Theo đề bài ta có DE\(\perp\)BC
Nên DE là đường cao thứ ba của tam giác OBC(3)
Từ (1),(2) và (3) suy ra:
Ba đường cao giao nhau tại một điểm trùng với điểm D
\(\Rightarrow\) 3 đường thẳng AC;DE;BK đồng quy(đpcm)

Dễ thấy:
\(AD = BC\) nhưng \(AD\) và \(BC\) không song song với nhau. Do đó hai vectơ \(\overrightarrow {AD} \) và \(\overrightarrow {BC} \) không bằng nhau.
\(CD > AB\) do đó hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \) không bằng nhau.
\(AC\) và \(BD\) không song song với nhau. Do đó hai vectơ \(\overrightarrow {AC} \) và \(\overrightarrow {BD} \) không bằng nhau.


