Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn B
Xét f(x) = x 4 - 38 x 2 + 120 x + 4 m trên đoạn [0;2] ta có:
Dấu “=” xảy ra khi và chỉ khi 
Nhận xét: Với trắc nghiệm thì ta thử đáp án được đáp án B
Chọn D
Xét 
trên đoạn [0;2], ta có:
Vậy 
Cách 1:
Nếu 4m > 0 thì 
Nếu 4m + 104 < 0
⇔
m < -126 thì 
Nếu 
thì 
Vậy có 27 số nguyên thỏa mãn.
Cách 2:
Khi đó 
Có 27 số nguyên thoả mãn.
Chọn đáp án D.
Xét y = x 4 - 38 x 2 + 120 x + 4 m trên đoạn 0 ; 2 ta có
Vậy
Có 27 số nguyên thoả mãn.
Chọn C
Tập xác định của hàm số là ℝ .
Ta có: 
Vì trên khoảng - 4 3 ; 0 hàm số đạt giá trị lớn nhất tại x = -1 nên hàm số đạt cực trị tại x = -1( cũng là điểm cực đại của hàm số) và a > 0.
Khi đó f'(x) = 0 
( đều là các nghiệm đơn)
Hàm số đạt cực đại tại x = -1 nên có bảng biến thiên:
=> x = - 3 2 là điểm cực tiểu duy nhất thuộc - 2 ; - 5 4
Vậy hàm số đạt giá trị nhỏ nhất tại x = - 3 2 trên đoạn - 2 ; - 5 4
Đặt t= x4- 1( -1≤ t≤ 15).
Khi đó hàm số trở thành: y= ( t+1) 2+ t2+ 5=2t2+ 2t+6
Đạo hàm y’ = 4t+ 2> 0 mọi x thòa mãn 0≤ x≤ 2
Hàm số đồng biến trên đoạn [0; 2].
Hàm số đạt giá trị lớn nhất tại x= 2 tức là t= 15, hàm số đạt giá trị nhỏ nhất tại x= 0 hay t=1
Chọn D.
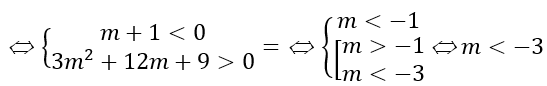
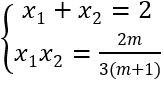
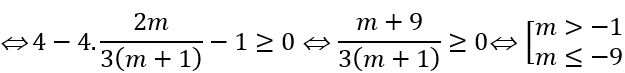
\(y'=4x^3+3ax^2+2bx\)
\(y'=0\Rightarrow x\left(4x^2+3ax+b\right)=0\Rightarrow\left[{}\begin{matrix}x=0\\4x^2+3ax+b=0\end{matrix}\right.\)
Xét \(g\left(x\right)=4x^2+3ax+b=0\) với \(\Delta=9a^2-16b\)
Hàm số luôn có 1 cực trị là \(x=0\), với \(y\left(0\right)=1\)
Dựa vào hình dáng đồ thị hàm bậc 4, để \(y\) đạt GTNN bằng 1 cũng chính là \(y\left(0\right)\) ta có các trường hợp sau:
- TH1: \(\Delta\le0\Rightarrow9a^2-16b\le0\Rightarrow b\ge\frac{9a^2}{16}\)
Khi đó \(S=a+b\ge a+\frac{9a^2}{16}=\frac{9}{16}\left(a+\frac{8}{9}\right)^2-\frac{4}{9}\ge-\frac{4}{9}\)
- TH2: \(g\left(x\right)=0\) có 2 nghiệm cùng âm \(x_1< x_2< 0\) và \(y\left(x_1\right)=1\)
\(\Rightarrow\left\{{}\begin{matrix}9a^2-16b>0\\\frac{b}{4}>0\\\frac{-3a}{4}< 0\\x_1^4+ax_1^3+bx_1^2+1=1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}b< \frac{9}{16}a^2\\b>0\\a>0\\x_1^2+ax_1+b=0\end{matrix}\right.\)
Nói chung ta ko cần tìm tiếp, do \(a;b>0\Rightarrow a+b>0>-\frac{4}{9}\)
TH3: \(g\left(x\right)=0\) có 2 nghiệm cùng dương \(0< x_1< x_2\) và \(y\left(x_2\right)=1\)
\(\left\{{}\begin{matrix}9a^2-16b>0\\\frac{b}{4}>0\\-\frac{3a}{4}>0\\y\left(x_2\right)=1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}b< \frac{9}{16}a^2\\b>0\\a< 0\end{matrix}\right.\)
\(y\left(x_2\right)=x_2^4+ax_2^3+bx_2^2+1=1\)
\(\Leftrightarrow x_2^2+ax_2+b=0\)
\(\Rightarrow\left\{{}\begin{matrix}4x_2^2+3ax_2+b=0\\x_2^2+ax_2+b=0\end{matrix}\right.\) \(\Rightarrow3x_2^2+2ax_2=0\Rightarrow x_2=-\frac{2a}{3}\)
\(\Rightarrow\frac{4a^2}{9}-\frac{2a^2}{3}+b=0\Rightarrow b=\frac{2a^2}{9}\)
\(\Rightarrow S=a+b=\frac{2a^2}{9}+a=\frac{2}{9}\left(a+\frac{9}{4}\right)^2-\frac{9}{8}\ge-\frac{9}{8}\)
So sánh 2 giá trị \(-\frac{4}{9}\) và \(-\frac{9}{8}\) ta được \(S_{min}=-\frac{9}{8}\) khi \(\left\{{}\begin{matrix}a=-\frac{9}{4}\\b=\frac{9}{8}\end{matrix}\right.\)