
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Đặt \(AB=a;AC=b\)
Xét \(\Delta ABC\) vuông tại A ta có :
Áp dụng hệ thức lượng trong \(\Delta\) vuông ta được :
\(\Leftrightarrow AH.BC=a.b\)
\(\Leftrightarrow ab=25.12=300\left(1\right)\)
Mặt khác:
Xét \(\Delta ABC\) vuông tại A, theo định lý Pytago ta được:
\(\Leftrightarrow a^2+b^2=BC^2\)
\(\Leftrightarrow a^2+b^2=625\)
\(\Leftrightarrow\left(a+b\right)^2-2ab=625\)
Thay \(\text{ab=}300\) vào ta được :
\(\Leftrightarrow\left(a+b\right)^2-600=625\)
\(\Leftrightarrow\left(a+b\right)^2=1225\)
\(\Rightarrow a+b=35\left(2\right)\)
Từ \(\left(1\right)\) và \(\left(2\right)\) \(\Rightarrow\) Giải phương trình ta được: \(\left\{{}\begin{matrix}a=15\\b=20\end{matrix}\right.\)
\(\Rightarrow AB=15;AC=20\)
Xét \(\Delta AHC\) vuông tại H, theo định lý Pytago ta được:
\(HC=\sqrt{AC^2-AH^2}=16\)
Ta có: \(AB.AC=AH.BC=12.25=300\left(1\right)\)
Lại có: \(AB^2+AC^2=BC^2=625\)
\(\Rightarrow\left(AB+AC\right)^2=AB^2+AC^2+2AB.AC=625+600=1225\)
\(\Rightarrow AB+AC=35\left(2\right)\)
Từ (1) và (2) \(\Rightarrow AB,AC\) là nghiệm của pt \(x^2-35x+300=0\)
\(\Rightarrow\left(x-20\right)\left(x-15\right)=0\) mà \(AB< AC\Rightarrow\left\{{}\begin{matrix}AB=15\\AC=20\end{matrix}\right.\)
Ta có: \(AC^2=CH.CB\Rightarrow CH=\dfrac{AC^2}{CB}=\dfrac{20^2}{25}=16\)
\(\Rightarrow D\)

\(\left(\sqrt{5-2\sqrt{6}}+\sqrt{2}\right)\cdot\dfrac{1}{\sqrt{3}}\)
\(=\sqrt{3}\cdot\dfrac{1}{\sqrt{3}}\)
=1

Câu 4b:
Ta có \(a-\sqrt{a}=\sqrt{b}-b\Leftrightarrow a+b=\sqrt{a}+\sqrt{b}\). (1)
Áp dụng bất đẳng thức Cauchy - Schwarz ta có:
\(a^2+b^2\ge\dfrac{\left(a+b\right)^2}{2};\sqrt{a}+\sqrt{b}\le\sqrt{2\left(a+b\right)}\).
Kết hợp với (1) ta có:
\(a+b\le\sqrt{2\left(a+b\right)}\Leftrightarrow0\le a+b\le2\).
Ta có: \(P\ge\dfrac{\left(a+b\right)^2}{2}+\dfrac{2020}{\left(\sqrt{a}+\sqrt{b}\right)^2}\) (Do \(a^2+b^2\ge\dfrac{\left(a+b\right)^2}{2}\))
\(=\dfrac{\left(a+b\right)^2}{2}+\dfrac{2020}{\left(a+b\right)^2}\) (Theo (1))
\(\Rightarrow P\ge\dfrac{\left(a+b\right)^2}{2}+\dfrac{2020}{\left(a+b\right)^2}\).
Áp dụng bất đẳng thức AM - GM cho hai số thực dương và kết hợp với \(a+b\le2\) ta có:
\(\dfrac{\left(a+b\right)^2}{2}+\dfrac{2020}{\left(a+b\right)^2}=\left[\dfrac{\left(a+b\right)^2}{2}+\dfrac{8}{\left(a+b\right)^2}\right]+\dfrac{2012}{\left(a+b\right)^2}\ge2\sqrt{\dfrac{\left(a+b\right)^2}{2}.\dfrac{8}{\left(a+b\right)^2}}+\dfrac{2012}{2^2}=4+503=507\)
\(\Rightarrow P\ge507\).
Đẳng thức xảy ra khi a = b = 1.
Vậy Min P = 507 khi a = b = 1.
Giải nốt câu 4a:
ĐKXĐ: \(x\geq\frac{-1}{2}\).
Phương trình đã cho tương đương:
\(x^2+2x+1=2x+1+2\sqrt{2x+1}+1\)
\(\Leftrightarrow\left(x+1\right)^2=\left(\sqrt{2x+1}+1\right)^2\)
\(\Leftrightarrow\left(x+1\right)^2-\left(\sqrt{2x+1}+1\right)^2=0\)
\(\Leftrightarrow\left(x+1-\sqrt{2x+1}-1\right)\left(x+1+\sqrt{2x+1}+1\right)=0\)
\(\Leftrightarrow\left(x-\sqrt{2x+1}\right)\left(x+\sqrt{2x+1}+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-\sqrt{2x+1}=0\left(1\right)\\x+\sqrt{2x+1}+2=0\left(2\right)\end{matrix}\right.\).
Ta thấy \(x+\sqrt{2x+1}+2>0\forall x\ge-\dfrac{1}{2}\).
Do đó phương trình (2) vô nghiệm.
Xét phương trình (1) \(\Leftrightarrow x=\sqrt{2x+1}\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\x^2=2x+1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\\left(x-1\right)^2=2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\\left[{}\begin{matrix}x-1=\sqrt{2}\\x-1=-\sqrt{2}\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\\left[{}\begin{matrix}x=\sqrt{2}+1>0>-\dfrac{1}{2}\left(TM\right)\\x=-\sqrt{2}+1< 0\left(\text{loại}\right)\end{matrix}\right.\end{matrix}\right.\).
Vậy nghiệm của phương trình là \(x=\sqrt{2}+1\).

c) Ta có: \(\left\{{}\begin{matrix}2x-6y=3\\\dfrac{2}{3}x-2y=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x-6y=3\\2x-6y=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}0x=0\\2x-6y=3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}0x=0\\6y=2x-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}0x=0\\y=\dfrac{2x-3}{6}\end{matrix}\right.\)(luôn đúng)
Vậy: Hệ phương trình có vô số nghiệm theo dạng \(\left\{{}\begin{matrix}x\in R\\y=\dfrac{2x-3}{6}\end{matrix}\right.\)
`2/3x-2y=1`
`<=>2x-6y=3`
Hoàn toàn trùng với phương trình trên
Vậy HPT có vô số nghiệm `x,y in RR`

d: góc CEB=góc CAB=90 độ
=>CEAB nội tiếp
góc EAC=góc EBC
góc ECA=góc EBA
mà góc EBC=góc EBA
nên góc EAC=góc ECA
=>EA=EC

Anh hoc lớp 1 hay lớp 9 vây anh ?
Câu này dể mà .
Toán lớp 1 luôn đó anh .
1 công 1 tức nhiên băng 2 rồi
Trần Ngọc Anh Tú: Đúng rồi đó thôi xuông lớp 1 đi em chị dạy cho




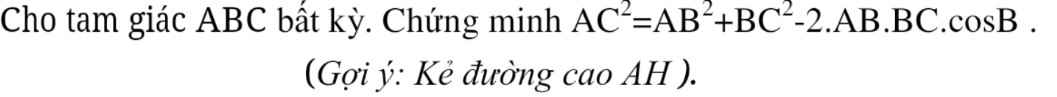
 Ai chỉ em với câu c với khó quá huhu
Ai chỉ em với câu c với khó quá huhu
Bài 3:
a: \(x^2-7=\left(x-\sqrt{7}\right)\left(x+\sqrt{7}\right)\)
d: \(x^2-16=\left(x-4\right)\left(x+4\right)\)
e: \(x-81=\left(\sqrt{x}-9\right)\left(\sqrt{x}+9\right)\)