
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



☭☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭ ☭

Bài 12:
a: Xét ΔABM và ΔACN có
AB=AC
\(\widehat{ABM}=\widehat{ACN}\)
BM=CN
Do đó: ΔABM=ΔACN

Chứng minh 2 tam giác chứa hai góc của tia phân giác đó bằng nhau, sau đó suy ra hai góc tương ứng. Suy ra tia phân giác

x thuộc - 6;-8;-5;-9
http://olm.vn/hoi-dap/question/131938.html
Bạn vào đây tham khảo nha !!!


\(B=\left(1-\frac{2}{5}\right)\left(1-\frac{2}{7}\right)\left(1-\frac{2}{9}\right)....\left(1-\frac{2}{99}\right)\)
\(B=\frac{3}{5}\cdot\frac{5}{7}\cdot\frac{7}{9}\cdot...\cdot\frac{97}{99}\)
\(B=\frac{3\cdot5\cdot7\cdot...\cdot97}{5\cdot7\cdot9\cdot...\cdot99}=\frac{3}{99}=\frac{1}{33}\)
Vậy B = \(\frac{1}{33}\)
\(\left[1-\frac{2}{5}\right]\left[1-\frac{2}{7}\right]\left[1-\frac{2}{9}\right]...\left[1-\frac{2}{99}\right]\)
\(=\frac{3}{5}\cdot\frac{5}{7}\cdot\frac{7}{9}\cdot...\cdot\frac{97}{99}\)
\(=\frac{3\cdot5\cdot7\cdot...\cdot97}{5\cdot7\cdot9\cdot...\cdot99}=\frac{3}{99}=\frac{1}{33}\)

10: Chọn B
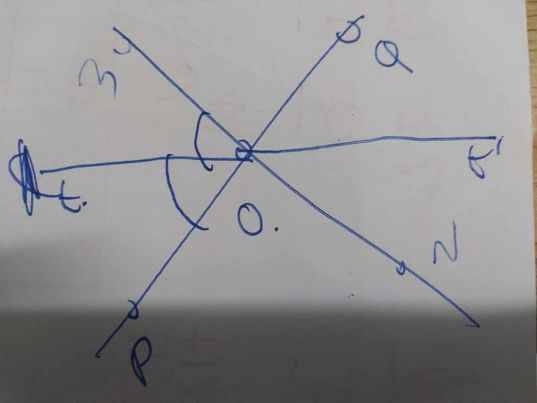
Ot là phân giác của \(\widehat{MOP}\)
=>\(\widehat{MOP}=2\cdot\widehat{tOP}\)
\(\widehat{MOP}=\widehat{NOQ}\)
=>\(\widehat{NOQ}=2\cdot\widehat{tOP}\)
mà \(\widehat{tOP}=\widehat{t'OQ}\)(hai góc đối đỉnh)
nên \(\widehat{NOQ}=2\cdot\widehat{t'OQ}\)
=>Ot' là phân giác của góc NOQ
11:
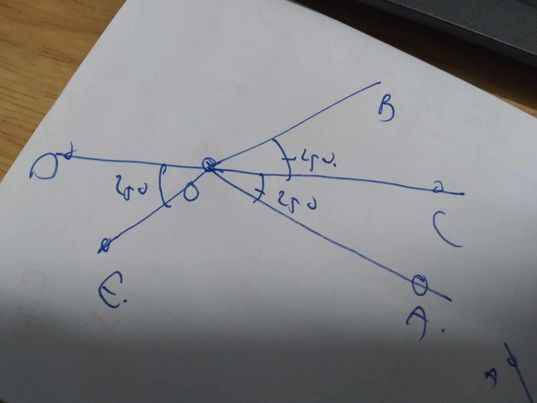
OC là phân giác của góc AOB
=>\(\widehat{AOC}=\widehat{BOC}=\dfrac{50^0}{2}=25^0\)
\(\widehat{DOE}=\widehat{BOC}\left(=25^0\right)\)
=>\(\widehat{DOE}+\widehat{DOB}=180^0\)
=>OB và OE là hai tia đối nhau
=>Hai góc đối đỉnh là \(\widehat{BOC};\widehat{DOE}\)
=>Chọn D
12:
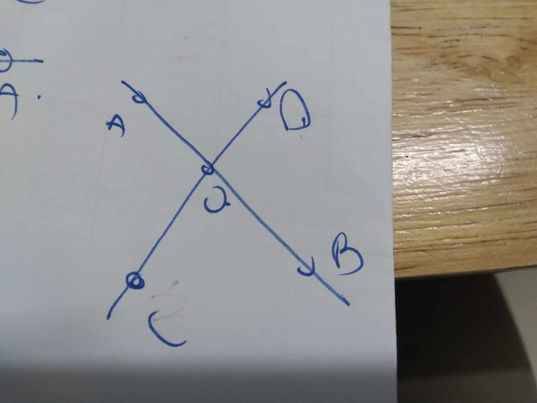
\(\widehat{AOC}+\widehat{AOD}=180^0\)
\(\widehat{AOC}-\widehat{AOD}=50^0\)
Do đó: \(\widehat{AOC}=\dfrac{180^0+50^0}{2}=115^0;\widehat{AOD}=115^0-50^0=65^0\)
=>\(\widehat{BOC}=\widehat{AOD}=65^0\)
=>Chọn B
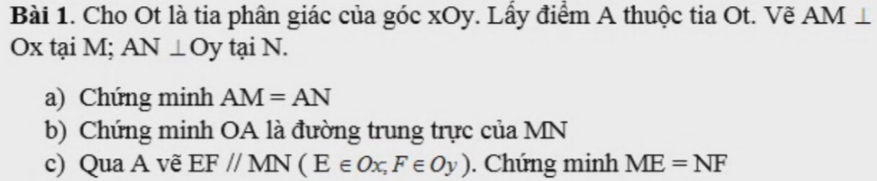 câu C thôi nhé. Nhanh hộ mìn
câu C thôi nhé. Nhanh hộ mìn


 h nhé
h nhé làm câu 10,11,12 chỉ vẽ hình thôi nếu giải thì giải hộ ạ
làm câu 10,11,12 chỉ vẽ hình thôi nếu giải thì giải hộ ạ