
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi \(\alpha\) là góc tạo với (d) và Ox
\(\Rightarrow tan\alpha=-1\)
\(\Rightarrow\alpha=135^0\)

Mình có cập nhật lại rồi, cậu xem lại coi có đề chưa nha

b, Ta có \(DE\cdot DF\cdot\cos E\cdot\cos F=DE\cdot DF\cdot\dfrac{DE}{EF}\cdot\dfrac{DF}{EF}=\dfrac{DE^2\cdot DF^2}{EF^2}\left(1\right)\)
Áp dụng HTL:\(DH\cdot EF=DE\cdot DF\Rightarrow DH=\dfrac{DE\cdot DF}{EF}\Rightarrow DH^2=\dfrac{DE^2\cdot DF^2}{EF^2}\left(2\right)\)
Từ (1)(2) ta được đpcm

b: DE//CF
=>sđ cung CD=sđ cung EF
góc AIB=1/2(sđ cung BD+sđ cung EF)
góc AOB=góc ACB=1/2*sđ cung BC
=1/2(sđ cung CD+sđcung DB)
=1/2(sđ cung EF+sđ cung DB)
=>góc AIB=góc AOB
=>AOIB nội tiếp
=>góc OIA=90 độ
=>I là trung điểm của DE

b) Để P nguyên thì \(\sqrt{x}+5⋮3\sqrt{x}-1\)
\(\Leftrightarrow3\sqrt{x}+15⋮3\sqrt{x}-1\)
\(\Leftrightarrow16⋮3\sqrt{x}-1\)
\(\Leftrightarrow3\sqrt{x}-1\in\left\{-1;1;2;4;8;16\right\}\)
\(\Leftrightarrow3\sqrt{x}\in\left\{0;2;3;5;9;17\right\}\)
\(\Leftrightarrow3\sqrt{x}\in\left\{0;3;9\right\}\)
\(\Leftrightarrow\sqrt{x}\in\left\{0;1;3\right\}\)
hay \(x\in\left\{0;1;9\right\}\)



c: \(=\left(4+\sqrt{3}\right)\cdot\sqrt{\left(4-\sqrt{3}\right)^2}\)
=(4+căn 3)(4-căn 3)
=16-3=13
d: \(=\sqrt{6+2\sqrt{5-2\sqrt{3}-1}}\)
\(=\sqrt{6+2\cdot\sqrt{4-2\sqrt{3}}}\)
\(=\sqrt{6+2\cdot\left(\sqrt{3}-1\right)}=\sqrt{4+2\sqrt{3}}=\sqrt{3}+1\)
b) \(\sqrt{\left(1-\sqrt{5}\right)^2}+\sqrt{23-8\sqrt{5}}\)
\(=\left|1-\sqrt{5}\right|+\sqrt{23-2\sqrt{60}}\)
\(=\sqrt{5}-1+\sqrt{\left(\sqrt{20}\right)^2-2.\sqrt{20}.\sqrt{3}+\left(\sqrt{3}\right)^2}\)
\(=\sqrt{5}-1+\sqrt{\left(\sqrt{20}-\sqrt{3}\right)^2}\)
\(=\sqrt{5}-1+\sqrt{20}-\sqrt{3}=\sqrt{5}+2\sqrt{5}-1-\sqrt{3}\)
\(=3\sqrt{5}-1-\sqrt{3}\)

b Ta có \(\Lambda ABE=\dfrac{1}{2}sđ\cap BE,\Lambda AFB=\dfrac{1}{2}sđ\cap BE\Rightarrow\Lambda ABE=\Lambda AFB\)
Mà \(\Lambda EAB=\Lambda BAF\) \(\Rightarrow\Delta EAB\sim\Delta BAF\left(g.g\right)\Rightarrow\dfrac{EA}{BA}=\dfrac{AB}{ÀF}\Rightarrow AE\cdot AF=AB^2\left(1\right)\)
Áp dụng hệ thức lượng giác vào \(\Delta AOB\) có:(BH vuông góc với AO)
\(\Rightarrow AH\cdot AO=AB^2\left(2\right)\)
Từ (1) và (2) \(\Rightarrow AH\cdot AO=AE\cdot AF\)
a) Xét tứ giác ABOC có
\(\widehat{ABO}\) và \(\widehat{ACO}\) là tứ giác nội tiếp
\(\widehat{ABO}+\widehat{ACO}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: ABOC là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
b) Xét (O) có
\(\widehat{BFE}\) là góc nội tiếp chắn \(\stackrel\frown{BE}\)
\(\widehat{ABE}\) là góc tạo bởi dây cung BE và tiếp tuyến BA
Do đó: \(\widehat{BFE}=\widehat{ABE}\)(Hệ quả góc tạo bởi tiếp tuyến và dây cung)
\(\Leftrightarrow\widehat{BFA}=\widehat{EBA}\)
Xét ΔBFA và ΔEBA có
\(\widehat{BFA}=\widehat{EBA}\)(cmt)
\(\widehat{ABF}\) là góc chung
Do đó: ΔBFA∼ΔEBA(g-g)
\(\Leftrightarrow\dfrac{AF}{AB}=\dfrac{AB}{AE}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(AB^2=AF\cdot AE\)(1)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔBOA vuông tại B có BH là đường cao ứng với cạnh huyền AO, ta được:
\(AB^2=AH\cdot AO\)(2)
Từ (1) và (2) suy ra \(AF\cdot AE=AH\cdot AO\)(đpcm)







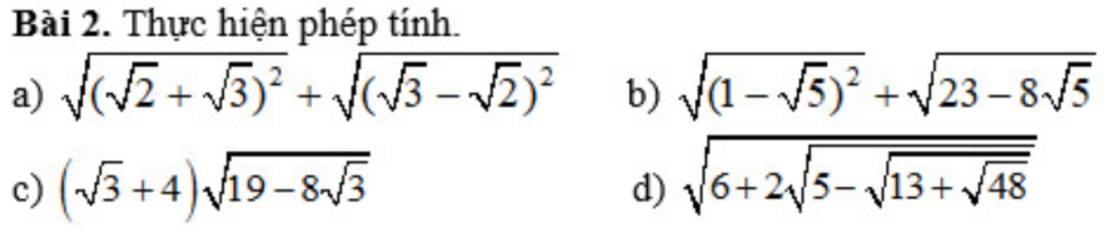 câu b, c, d thôi ạ!
câu b, c, d thôi ạ!
xét tg CHA và tg CAB
BCA chung
CHA=CAB=90
=>tg CHA đồng dạng CAB(gg)
=>CH/CA=CA/CB
=>CH.CB=CA2(1)
cm tương tự tg CKA đồng dạng tg CAD(gg)
=>CK/CA=CA/CD
=>CK.CD=CA2(2)
từ (1)(2)=>CH.CB=CK.CD
=>CH/CD=CK/CB
xét tg CKH và tg CBD
CH/CD=CK/CB
=>tg CKH đồng dạng tg CBD
Ms nộp bài xong, nhưng vẫn cảm ơn bạn nha!